hier habe etwas veruch, bitte wenn falsch , kannst du es ignoerieren, ich wollte GENAU SO wie oben im Buch die gleich Nethode mit Fraben machen: hir mein Versuch.
Text erkannt:
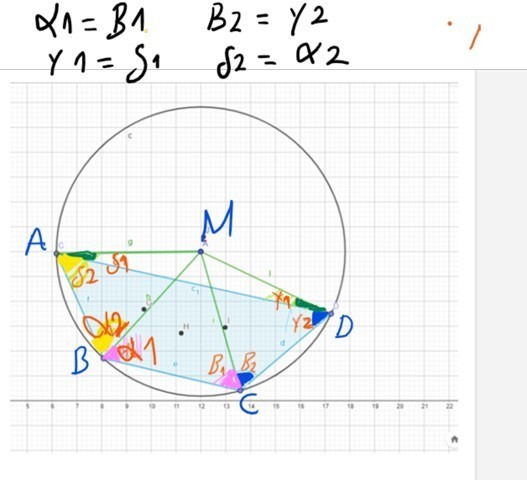
\( \begin{array}{ll}\alpha_{1}=B_{1} & B_{2}=y_{2} \\ y_{1}=\delta_{1} & \delta_{2}=\alpha_{2}\end{array} \)
KÖdung

Text erkannt:
Behauptang \( \quad \alpha+y=180 \)
\( B+\delta=180 \)
Beweis:
Verbinden MiselpunicM) \( m \) it Eck punkte \( A, B, C, D \).
Drerecle \( A B M ; B \subset M \),
sind gleichschenk, ADM
wíl MA, MB, \( \overline{M C}, \overline{M D} \)
sindoradien cles unikrases.
and sind gleich lang.
\( \alpha_{1}=B_{1} \quad \beta_{2}=y 1+y^{2} \)
\( y_{1}=\delta 1 \quad x_{2}=\delta 1+\delta 2 \)
Durch zerlegung ron sehemsvieredk sind Jerzt 6 winkJ, Pairbt man glach grober mikel, benotigt man Nur 3 Farben \( \{ \) diese sind

Text erkannt:
glach grober Winkel, benơtigt man Nur 3 Farben \( \{ \) diese sind gelb, l, la and blu\} deé Farbe grüid gas gehiort nicht dazu weil es gehort nicht zum viereck \( \{A, B, C, 0\} \) und in den zwei gegenver liegendes wrintel (x) wit winkel \( \underset{\substack{\alpha \\\left(\alpha+\alpha_{2}\right)}}{ } \) und y2 kommen \( \left(\alpha 1+\alpha_{2}\right) \) ei Farben \( \{ \) gelb, lila, blark \( \left(\alpha_{1}+\alpha_{2}\right) \) \( \left(B_{1}+B_{2}\right) \)

Text erkannt:
Jetz rechucischpectan
\( \begin{aligned} \alpha+y_{2} &=\alpha_{1}+\alpha_{2}+y_{2} \\ &=B_{1}+S_{1}+S_{2}+\alpha_{1}=B_{1} \\ &=B_{1}+S_{1}+S_{2}+\left(B_{2}-y_{1}\right) \beta_{2}=y_{1}+y_{2} \\ &=B_{1}+S_{1}+S_{2}+\beta_{2}-y_{1} y_{1}=S_{1} \\ &=B_{1}+B_{2}+S_{1}+S_{2}-y_{1} \alpha_{2}=S_{1}+S_{2} \\ &=B^{*}+S_{2}+S_{1}-y_{1} \\ &=B+S_{2}+0^{*} \\ &=B_{2}+S_{2} \\ \forall &=\beta_{2}+S_{2} \end{aligned} \)
Da de winkelsumme in viereck insgesamt \( 360^{\circ} \) sind damn leweils zores gegonuban liegonden

Text erkannt:
\( =B^{\prime}+S_{2}+S_{1}-y_{1} \)
\( =B+S_{2}+0^{\prime} \)
\( =\beta+S 2 \)
\( \alpha+y_{2}=\beta+\beta_{2} \)
Da de winkelsumme in vieredk insgesumt \( 360^{\circ} \cdot \) sind domn jeweils zurel gegeniber lizsonden Winkel Zan. zusamen \( 180^{\circ} \)
\( \begin{aligned} x+y 2 &=3+\int \limits_{2} 2 \\ 180 &=180 \end{aligned} \)