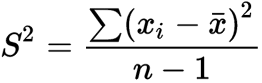Aufgabe: In einer Stadt wurde von der Abteilung für Soziales die Zahl der Kinder pro Haushalt erhoben:
Kinderzahl
| Anzahl der Haushalte
|
0
| 110
|
1
| 140
|
2
| 90
|
3
| 45
|
4
| 10
|
5
| 5
|
Berechnen Sie die adäquaten Lage- und Streuungsmaße!
Problem/Ansatz:
Die Lösungen stehen bereits da, aber ich weiß nicht genau wie man darauf kommt. Ich hab die Formel für die Varianz angehangen, aber bin mir nicht sicher ob das die richtige ist.
Gesucht werden also Mittelwert, Varianz und Standardabweichung.
Wenn ich den Mittelwert berechne komme ich auf genau 1,3 aber als Lösung wird 1,34 angegeben. Muss ich nicht alle Werte zusammenrechnen und durch n=400 teilen? Also:
((0*100)+(1*140)+(2*90)+......) / 400 = 1,3
Wieso 1,34?
Dann bei der Varianz hab ich keine Ahnung wie man auf die angegebene Lösung von s² = 1,29 kommen soll (ich weiß dass die Standardabweichung einfach nur die Wurzel aus der Varianz ist).
Wie berechne ich die Varianz in dem Fall?
Was ich versucht habe war die angehängte Formel zu nutzen, also die Summen aus den einzelnen Werten zu bilden, die mit dem Mittelwert subtrahiert und dann quadriert wurden.
(0-1,3)² + (1-1,3)² + (2-1,3)² + ...
Und das dann durch n-1, also 6-1 bzw. 5.
Damit komme ich aber auf eine absurd hohe Zahl von 26,14 durch 5, was 5,228 ergibt und nicht die in der Lösung angegebenen 1,29. Wie zur Hölle kommt man auf eine Varianz von 1,29?
Text erkannt:
\( S^{2}=\frac{\sum\left(x_{i}-\bar{x}\right)^{2}}{n-1} \)
rr