Hinweis: Die Beschriftung der Skizze kann nicht stimmen. Wenn man davon ausgeht, dass die gedruckten Angaben gegeben sind, dann muss die Skizze so aussehen:
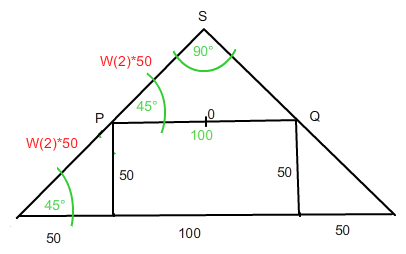
[ W(2) steht für √ ( 2 ) ]
In schwarz habe ich die gegebenen Werte gesetzt.
In grün habe ich diejenigen Werte gesetzt, die in der von dir fotografierten Skizze handschriftlich eingetragen wurden (also vermutlich berechnet wurden) und die korrekt sind. In rot hingegen habe ich die korrekten Werte für diejenigen Werte gesetzt, die in jener Skizze falsch berechnet wurden.
Lege nun das Dreieck so ins Koordinatensystem, dass der Ursprung 0 in der Mitte der Basis des kleinen aufgesetzten Dreiecks liegt (siehe meine Skizze).
Die beiden Punkte P und Q, die durch die neue Straße verbunden werden sollen, haben dann die Koordinaten
P ( - 50 | 0 ) und Q ( 50 | 0 )
Wählt man nun als Funktion für das Verbindungsstück eine Parabel, so kann man deren Funktionsgleichung aufgrund der "geschickten" Wahl der Lage des Koordinatensystems nun in der Nullstellenform angeben, also:
f ( x ) = a ( x - 50 ) ( x + 50 )
und muss nur noch den Parameter a bestimmen. Dieser muss so gewählt werden, dass f ( x ) in den Punkten P und Q dieselbe Steigung hat wie das jeweils dort liegende gerade Straßenstück.
Das Straßenstück in Punkt P hat die Steigung 1 (45 ° - Winkel zur Horizontalen), also muss gelten:
f ' ( - 50 ) = 1
Die Ableitung von f ist :
f ' ( x ) = a * 2 * x
es muss also gelten:
f ' ( - 50 ) = a * 2 * ( - 50 ) = 1
<=> a = - 1 / 100
und somit ist die gesuchte Funktion:
f ( x ) = ( - 1 / 100 ) * ( x - 50 ) * ( x + 50 )
bzw. in Normalform:
f ( x ) = ( - 1 / 100 ) x 2 + 25