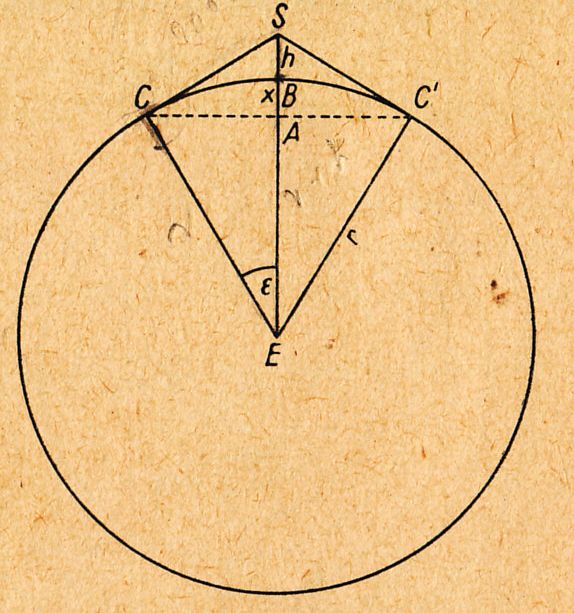
Aufgabe: Wie groß ist die Aussichtsweite BC und wie groß das Stück der Erdoberfläche, das man von der Schneekoppe h = 1600 m überblicken kann, wenn die Aussichtsweite BC infolge der atmosphärischen Strahlenbrechung um 8% vergrößert wird ( r = 6370 km, 2 π r = 40.000 km).
Ich kann ε = 1,28° berechnen, auch BC plus Strahlenbrechung. Doch ich kann nur den Schritten I und II der Lösung im Lehrbuch folgen.
Ich bitte um Hilfe, die weiteren zu verstehen:
I. cos ε = r / (r+h), ε = 1,28°
II. ε / 360 = BC / 40.000. BC = 145 km, mit Strahlenbrechung 157 km
III. O = 2 π r x
IV. cos ε = (r – x) / r
I/IV. x = r – (r2 / ( r + h)) = rh / (r + h)
I/IV/III. O = (2 π r2 h) / (r + h) = 64.022 km2, mit Strahlenbrechung 160.531 km