Aufgabe:
Ich habe eine Art des "Traveling Salesman Problems" vorliegen, bei welchem bestimmte Routen jedoch fest definiert sind, sprich es gibt Kanten, welche bereits vordefiniert sind und nicht "optimiert" werden dürfen, z.B. wenn eine Ware von A nach B muss lautet die Kante (a,b). Die Wege zu A bzw. von B weg zu den weiteren fixen Kanten oder anderen Punkten sind jedoch variabel. Die Skizze hier soll es nochmal verdeutlichen:
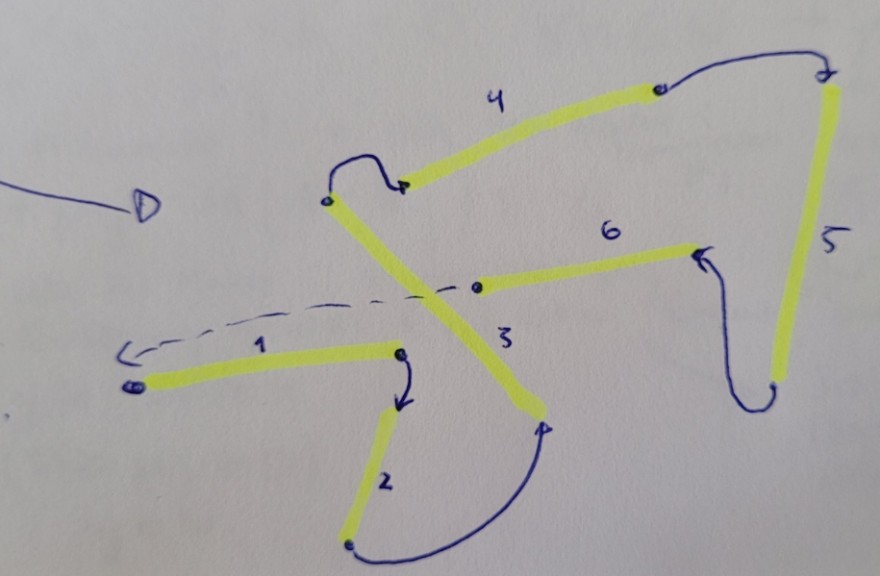
Zur Erklärung: die Routen in gelb sind feste Routen, welche nicht verändert werden können. Sehr wohl können jedoch die Wege zwischen den Routen optimiert werden, sodass am Ende die gefahrene Distanz (und weitere Parameter, auf welche hier jetzt nicht weiter eingegangen wird) minimal sind.
Das Ganze wird als Graph dargestellt. Die Menge ist definiert als: \( A=\left\{(i, j) \in V \times V: a_{i}+t_{i j} \leq b_{j}, i, j \neq o\right\} \)
Problem/Ansatz:
Wie kann ich die Menge darstellen um die fixierten Routen (i,j) als zwingende Voraussetzung zu definieren bzw. die Auswahlmöglichkeit auf die Routen zwischen den Anfangs- und Endpunkten zu beschränken?