"Verkohltes Allerlei" und "Grünkohl-Schwefel-Saft"

Question

Aufgabe:

Die örtliche Fressmeile ist besonders zu empfehlen. Dort findet man fein säuberlich aufgereiht fünfzig Restaurants. In dreißig dieser Restaurants wird die lokale Spezialität "Verkohltes Allerlei" angeboten. Die Getränke-Spezialität "Grünkohl-Schwefel-Saft" steht in vierzig der Restaurants auf der Getränkekarte. Lediglich fünf Restaurants verwehren sich den örtlichen kulinarischen Vorlieben und bieten weder "Verkohltes Allerlei" noch "Grünkohl-Schwefel-Saft™ an.

a) Stelle die Situation grafisch in einem Venn-Diagramm dar.

b) Bestimme die Wahrscheinlichkeit dafür, dass man beim Besuch eines zufällig ausgewählten Restaurants dieser örtlichen Fressmeile sowohl die Speise "Verkohltes Allerlei als auch das Getränk "Grünkohl-Schwefel-Saft" bestellen kann.

Problem/Ansatz:

hey ich bin neu auf der Plattform und bin gespannt wie dies so abläuft. Ich habe Schwierigkeiten mit mathe vorallem mit Stochastik. Dort verstehe ich garnichts. Kann mir bitte geholfen werden. LG : )

Comments

mit Stochastik. Dort verstehe ich garnichts

Dann wird es ja sicher mit dem Venn-Diagramm geklappt haben. Wie schaut Deines denn aus?

Ich würde behaupten, dass in der grünen Schnittmenge 30 + 40 - 45 Restaurants sind. Die Formel dazu steht üblicherwiese als "Additionssatz der Mengenlehre" in den Lehrbüchern, in der Form 30 + 40 - x = 45

Answer 1

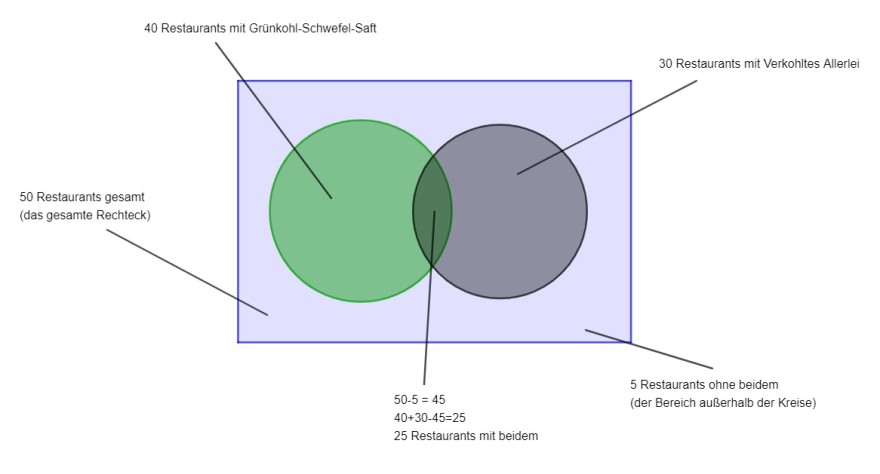
Das Venn-Diagramm ist, denke ich, selbsterklärend.

Wir wissen:

Es gibt 50 Restaurants, 5 mit keiner der beiden Speisen, 40 mit dem Saft, 30 mit dem Allerlei. Deswegen gibt es 45 mit zumindest einem von beiden. Damit wir die 40-Mal Saft und die 30-Mal Allerlei auf diese 45 Restaurants verteilen können, müssen 25 Restaurants beiden servieren. So ergibt sich: 25 beides, 15 nur Saft, 5 nur Allerlei, 5 nix.

Für b) rechnest du dann: 25/50=1/2=0.5

Die Wahrscheinlichkeit ist also 50%.

Anmerkung, wie man auf die 25 kommt, falls das nicht klar ist. Betrachte das folgende Gleichungssystem, wobei B die Restaurants sind in denen beides serviert wird, S nur Saft und A nur Allerlei:

$$\begin{aligned}\text{I}:\quad 2B+S+A&=70\\\text{II}:\quad B+S+A&=45\end{aligned}\begin{cases}\text{Aus I-II folgt B=25 und daraus direkt auch}\\\text{ S=15 und A=5 weil 40-25 respektive 30-25 diese Ergebnisse liefern}\end{cases}$$

Auf die erste Gleichung kommt man durch die Überlegung: Stell dir vor du gehst von Restaurant zu Restaurant machst einen Strich jedes Mal wenn ein Restaurant Saft serviert und einen, wenn sie Allerlei servieren. Bei B machst du also 2 Striche, bei A einen und bei S einen. Insgesamt kommst du auf 30+40=70 Striche.

Auf die zweite Gleichung kommt man, weil ja 50-5=45 Restaurants zumindest eins servieren müssen, wenn nur 5 keins servieren. Und diese Anzahl ist eben die Summe aus den Restaurants, die entweder nur Saft, nur Allerlei oder beides servieren.