Zeige, dass für alle a,b,c>0 gilt, dass c/a+a/(b+c)+b/c >= 2

Question

Zeige, dass für alle \( a, b, c \in \mathbb{R}_{>0}^{+}: \frac{c}{a}+\frac{a}{b+c}+\frac{b}{c} \geq 2 \) gilt

Problem/Ansatz:

Ich weiß einfach nicht, wie man bei so etwas vorgeht bzw. wie man so etwas beweist.

Comments

Die 3 in der Überschrift ist falsch, wie die Probe mit a=b=c=1 beweist.

In der Ungleichung steht sicher die 2 aus dem Text unter der Überschrift.

---

Korrigiert       .

Answer 1

Hallo,

addiere auf beiden Seiten eine "Trick-Eins" \(\frac{c}{c}=1\), dann hast du:$$\frac{c}{a}+\frac{a}{b+c}+\frac{b+c}{c}\geq 3$$ Und dann kannst du die AM-GM-Ungleichung anwenden.

Comments

Ok hört sich schon mal gut an der Trick ^^

Wie genau die AM-GM-Ungleichung?

---

Drei Variablen, Zahl 3 auf der anderen Seite, komische Ungleichung => Alles Indikatoren für AM-GM. Ich hab die drei hier natürlich provoziert, aber da kommt man vielleicht noch drauf.

Es gilt ja: \(\frac{x_1+x_2+x_3}{3}\geq \sqrt[3]{x_1x_2x_3} \Leftrightarrow x_1+x_2+x_3\geq 3\sqrt[3]{x_1x_2x_3}\)

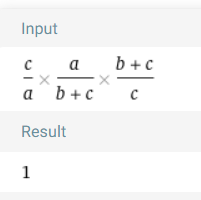
Setz einfach \(x_1=\frac{c}{a}\), \(x_2=\frac{a}{b+c}\) und \(x_3=\frac{b+c}{c}\). Der Clou ist nämlich, dass \(x_1x_2x_3=1\) ist, probier's mal aus. Multipliziere die drei Summanden nach der Trick-Eins rechts miteinander, das hebt sich alles zu 1 auf.

---

Ist 1 nicht kleiner als 3?

Der Term soll doch größer gleich 3 sein.

---

\( x_1+x_2+x_3\geq 3\underbrace{\sqrt[3]{x_1x_2x_3}}_{=1}\)

Also \(3\cdot 1\)