Ein Wassertropfen der Höhe h und Radius r kann durch einen Kegel modeliert werden, der auf einer Halbkugel sitzt.
a) Bestimmen Sie die Höhe eines Wassertropfens mit Radius r = 2 mm und Volumen V = 8π mm³.
V = 1/2·4/3·pi·r^3 + 1/3·pi·r^2·(h - r) = 1/3·pi·r^2·(h + r)
h = (3·V - pi·r^3)/(pi·r^2)
Nun einsetzen und ausrechnen
h = (3·(8·pi) - pi·2^3)/(pi·2^2) = 4 mm
b) Beschreiben Sie einen halben Wassertropfen mit Höhe h und Radius r durch eine
Funktion f : [0, h] × [−r, r] → R. Berechnen Sie dessen Volumen per Intergration.
Abweichend von der Aufgabenstellung hätte ich den halben Regentropfen mit einer Funktion wie folgt beschrieben:
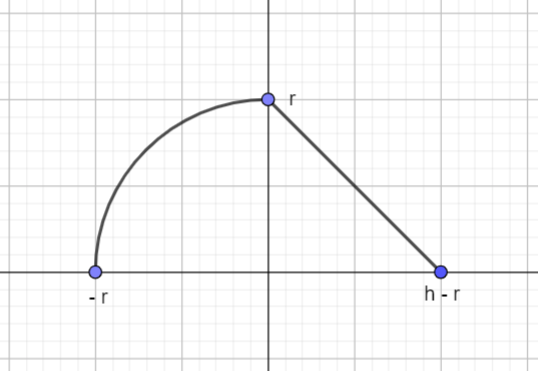
Davon hätte ich dann das Rotationsintegral berechnet.