Heisst, dass hier erwähnte bel, aber feste x0 e X, dass gleich mehrere y e Y auf dieses xo abgebildet werden oder …

Question

Aufgabe:

die Problemstellung ist als Bild hochgeladen. ( selbst "verfasst" bzw. aus dem Skript abgeschrieben )

Problem/Ansatz:

Heisst, dass hier erwähnte bel, aber feste x0 e X, dass gleich mehrere y e Y auf dieses xo abgebildet werden oder ist das völlig falsch?

Eine allgemeine Frage:

Heisst es in diesem Kontext, dass eine Abbildung S : X --->Y, immer ALLE x e X einbezieht? So dass bei einer injektiven Funktion auch alle x e X abgebildet werden, aber ein y e Y frei bleibt. Also y e Y \ f(X). Werden immer alle x e X abgebildet?

Also das X immer "nur" genau die Definitionsmenge umfasst.

LG

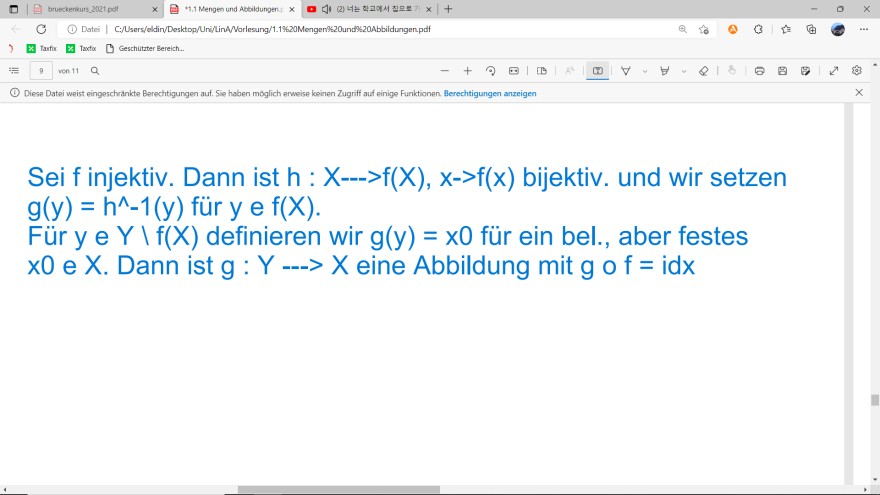
Text erkannt:

Sei \( f \) injektiv. Dann ist \( h: X \rightarrow>f(X), x->f(x) \) bijektiv. und wir setzen \( g(y)=h^{\wedge}-1(y) \) für \( y \) e \( f(X) \).
Für y e \( Y \backslash f(X) \) definieren wir \( g(y)=x 0 \) für ein bel., aber festes \( x 0 \) e \( X \). Dann ist \( g \) : \( Y \ldots X \) eine Abbildung mit \( g \) o \( f=i d x \)

Answer 1

dass eine Abbildung S : X --->Y, immer ALLE x e X einbezieht?

Ja, das steckt in der Definition: Zu jedem x∈X gibt es genau ein

y∈Y mit S(x)=y,  Die y müssen dabei allerdings nicht alle drankommen,

können aber. Dann ist die Funktion surjektiv.

Comments

die y e Y\f(X) die nicht getroffen werden durch die Festlegung y e Y\f(X) mit g(y)=x0 mit x0 fest aber beliebig, dann trotzdem getroffen werden.

Nein, die werden durch f nicht getroffen; denn sie sind ja aus Y\f(x).

Aber die Abbildung g ist auf Y definiert und für g o f gilt,

dass es id_X ist.