Wendepunkt der Funktion f(x) = 3x^4 - 4x^3

Question

Aufgabe:

Wendepunkt des Graphen bestimmen

f(x)=3x^4-4x³

Problem/Ansatz:

Irgendwie versteh ich das nicht ganz

Die Ableitungen:

f‘(x)=12x³-12x²

f“(x)=36x²-24x

f“‘(x)=72x-24

Die Nullstelle von der zweiten Ableitung ist x=0 und x1=0,667. diese Funktion hat jetzt 2 nullstellen und ich weiß leider nicht was ich machen soll bzw vorgehen soll

Comments

Mögliche Wendestellen hast du also bei x = 0 und x = \( \frac{2}{3} \).

Du kannst jetzt deine Ergebnisse in die 3. Ableitung einsetzen, denn wenn f'''(x₀) ≠ 0, hat der Graph an dieser Stelle einen Wendepunkt.

f'''(0) = -24 und f'''(\( \frac{2}{3} \)) = 24

Setze dann die x-Werte der Wendestellen noch in f(x) ein, um die y-Koordinate der Punkte zu bestimmen.

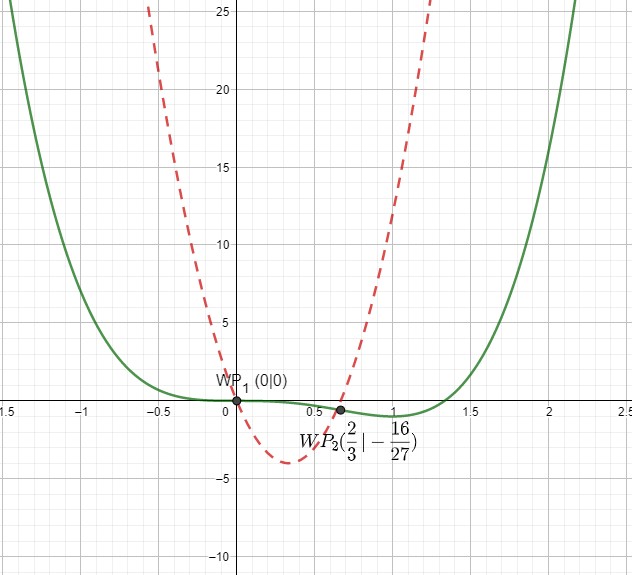Im Bereich zwischen den Punkten ist der Graph von f rechtsgekrümmt, da f''(x) < 0, sonst linksgekrümmt.

WP1 ist auch Terrassen-/Sattelpunkt, da auch f'(0) = 0

Answer 1

Wen interessieren die Nullstellen der ersten Ableitung, wenn du die Wendestelle bestimmen sollst???

Du hast gerade mal potenzielle Extremstellen gefunden.

Übrigens ist das hier

Die Nullstelle von der ersten Ableitung ist x=0 und x1=0,667.

falsch. Da darf nicht 0,667 stehen, wo exakte \( \frac{2}{3} \) hingehören.

Comments

Ich hab es falsch hingeschrieben das sind die nullstellen der 2. Ableitung

---

Dann KÖNNTE es Wendestellen bei x=0 und bei x=2/3 geben.

Hast du an diesen Stellen schon den Wert der dritten Ableitung berechnet?

---

Also bei der nullstelle 0 ist es -24, und ich weiß halt nicht wie ich da vorgehen soll ob ich ein VZW anwenden soll und wenn wie

Bei 2/3 habe ich auch schon den Wendepunkt ausgerechnet WP(0,667/-0,593)

---

Bei 2/3 habe ich auch schon den Wendepunkt ausgerechnet WP(0,667/-0,593)

Nochmal langsam zum Mitschreiben: 2/3 ist 2/3 und nicht 0,667.

Demzufolge ist 3*(2/3)^4-4*(2/3)^3 auch nicht -0,593, sondern sehr exakt (nach dem Kürzen) ein Bruch mit dem Nenner 27.

Answer 2

zweiten Ableitung ... diese Funktion hat jetzt 2 nullstellen und ich weiß leider nicht was ich machen soll

Du solltest in Erwägung ziehen, dass der Funktionsgraph vielleicht zwei Wendepunkte haben könnte.

Answer 3

Wendepunkt des Graphen bestimmen

f(x) = 3·x^4 - 4·x^3
f'(x) = 12·x^3 - 12·x^2
f''(x) = 36·x^2 - 24·x = 12·x·(3·x - 2) = 0 --> x = 0 ∨ x = 2/3 (beides sind einfache Nullstellen und damit wirkliche Wendestellen.)

f(0) = 0 → WP1(0 | 0)

f(2/3) = - 16/27 → WP2(2/3 | - 16/27)

Wir finden also 2 Wendepunkte.

Answer 4

Da es sich hier um eine ganzrationale Funktion 4 Grades handelt, die einen Sattelpunkt im Ursprung hat,
kannst du die x-Koordinate des Wendpunktes ganz einfach bestimmen, indem du den Abstand zur nächsten Nullstelle durch 2 teilst.

Der Taschenrechner spuckt dir 4/3 als zweite Nullstelle aus.

Wenn du das nun durch 2 teilst hast du 2/3. Das ist die x-Koordinate des WP, dadurch hast dir den ganzen Aufwand mit den blöden Ableitungen gespart.

Nun einfach die 2/3 in die Stammfunktion einsetzen, und dann bekommst du die y-Koordinate für den WP.