Text erkannt:
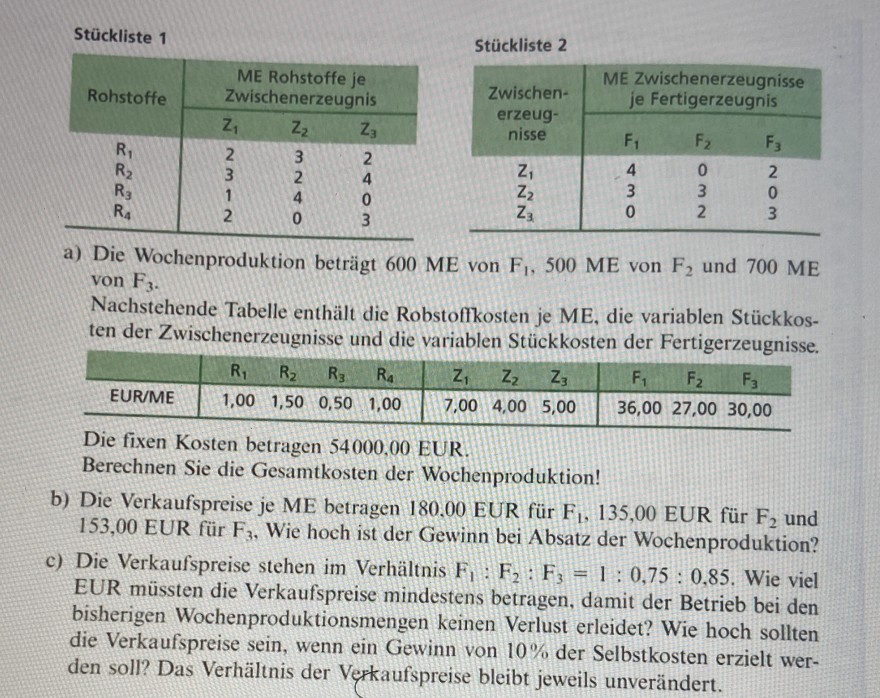
Stückliste 1
\begin{tabular}{|c|ccc|}
\multirow{3}{*}{ Rohstoffe } & \multicolumn{3}{|c|}{ ME Rohstoffe je Zwischenerzeugnis } \\
\cline { 2 - 4 } & \( Z_{1} \) & \( Z_{2} \) & \( Z_{3} \) \\
\( R_{1} \) & 2 & 3 & 2 \\
\( R_{2} \) & 3 & 2 & 4 \\
\( R_{3} \) & 1 & 4 & 0 \\
\( \mathbf{R}_{4} \) & 2 & 0 & 3 \\
\hline
\end{tabular}
a) Die Wochenproduktion beträgt \( 600 \mathrm{ME} \) von \( \mathrm{F}_{1}, 500 \mathrm{ME} \) von \( \mathrm{F}_{2} \) und \( 700 \mathrm{ME} \) von \( \mathrm{F}_{3} \).
Nachstehende Tabelle enthält die Robstoffkosten je ME, die variablen Stückkosten der Zwischenerzeugnisse und die variablen Stückkosten der Fertigerzeugnisse.
\begin{tabular}{c|cccc|ccc|ccc}
& \( R_{1} \) & \( R_{2} \) & \( R_{3} \) & \( R_{4} \) & \( Z_{1} \) & \( Z_{2} \) & \( Z_{3} \) & \( F_{1} \) & \( F_{2} \) & \( F_{3} \) \\
\hline EUR/ME & 1,00 & 1,50 & 0,50 & 1,00 & 7,00 & 4,00 & 5,00 & 36,00 & 27,00 & 30,00 \\
\hline
\end{tabular}
Die fixen Kosten betragen 54000,00 EUR.
Berechnen Sie die Gesamtkosten der Wochenproduktion!
b) Die Verkaufspreise je ME betragen 180,00 EUR für \( \mathrm{F}_{1}, 135,00 \) EUR für \( \mathrm{F}_{2} \) und 153,00 EUR für \( \mathrm{F}_{3} \). Wie hoch ist der Gewinn bei Absatz der Wochenproduktion?
c) Die Verkaufspreise stehen im Verhältnis \( F_{1}: F_{2}: F_{3}=1: 0,75: 0,85 \). Wie viel EUR müssten die Verkaufspreise mindestens betragen, damit der Betrieb bei den bisherigen Wochenproduktionsmengen keinen Verlust erleidet? Wie hoch sollten die Verkaufspreise sein, wenn ein Gewinn von \( 10 \% \) der Selbstkosten erzielt werden soll? Das Verhältnis der Verkaufspreise bleibt jeweils unverändert.
Aufgabe: