Aufgaben zur Integralrechnung - Kontrolle

Question

Die Aufgabe hier lautete die Funktion zu integrieren.

Ich wollte fragen, ob das alles richtig gemacht wurde (und wenn ja wieso e^x-1 integriert immernoch e^x-1 ist, aber bei der zweiten Aufgabe was anderes rauskommt, als die Ausgangsfunktion)

Falls es aber falsch ist, könnte mir bitte jemand erklären wie es richtig gemacht werden würde.

Vielen Dank im Voraus und einen schönen Abend noch.

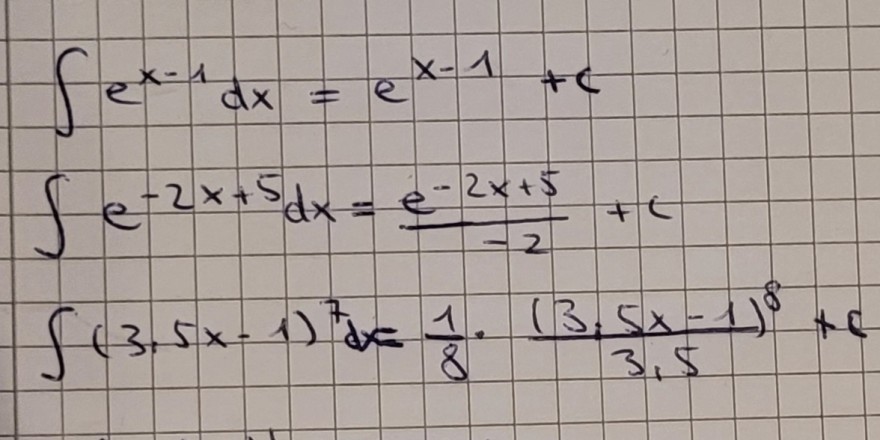
Text erkannt:

\( \int e^{x-1} d x=e^{x-1}+c \)
\( \int e^{-2 x+5} d x=\frac{e^{-2 x+5}}{-2}+c \)
\( \int(3,5 x-1)^{7} d x=\frac{1}{8} \cdot \frac{(3,5 x-1)^{8}}{3,5}+c \)

Answer 1

Leite die rechte Seite ab.

Falls es aber falsch ist

Es ist nicht falsch.

Comments

Ist auch die letzte Aufgabe richtig?

Weil beim ableiten des Ergebnisses komme ich irgendwie nicht auf die Stammfunktion.

---

Weil beim ableiten des Ergebnisses komme ich irgendwie nicht auf die Stammfunktion.

Die Stammfunktion steht rechts vom Gleichheitszeichen. Und wenn du die ableitest, dann kommt die Funktion unter dem Integral heraus.

Das sieht also alles richtig aus. Benutze auch zur Kontrolle immer einen Integralrechner oder auch einen Ableitungsrechner.

Answer 2

\( \int e^{x-1} \cdot d x \)
Substitution:
\( \begin{array}{l} u=x-1 \rightarrow \rightarrow x=u+1 \rightarrow \rightarrow d x=1 \cdot d u \\ \int e^{x-1} \cdot d x=\int e^{u} \cdot d u \end{array} \)
Re-Substitution:
\( \int e^{-2 x+5} \cdot d x \)
Substitution:
\( u=-2 x+5 \rightarrow \rightarrow 2 x=5-u \rightarrow \rightarrow x=\frac{5}{2}-\frac{u}{2} \rightarrow \rightarrow d x=-\frac{1}{2} \cdot d u \)
\( \int e^{-2 x+5} \cdot d x=\int e^{u} \cdot\left(-\frac{1}{2}\right) \cdot d u=-\frac{1}{2} \cdot \int e^{u} \cdot d u=-\frac{1}{2} \cdot e^{u} \)
Re-Substitution:
\( \int e^{-2 x+5} \cdot d x=-\frac{1}{2} \cdot e^{-2 x+5}+C \)