Hallo,
mache Dir nochmal eine (saubere) möglichst massstabsgetreue Zeichnung
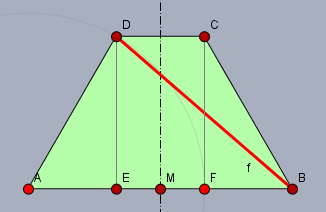
Das ist ein symmetrisches Trapez, weswegen die Fußpunkte \(E\) und \(F\) ebenfalls symmetrisch zur Mitte \(M\) liegen. Weiter ist $$|EF| = |CD| = a$$und daraus und aus \(|AB| = 3a\) folgt$$|AE| = |EF| = |FB| = a$$Im Dreieck \(\triangle AED\) gilt nach Pythagoras$$\begin{aligned}|AE|^2 + |ED|^2 &= |AD|^2\\ a^2 + |ED|^2 &= (2a)^2 && |\,-a^2 \\|ED|^2 &= 3a^2 \end{aligned}$$Und im Dreieck \(\triangle EBD\) gilt (Die Diagonale sei \(f\)) $$\begin{aligned}f^2 &= |ED|^2 + |EB|^2 \\ f^2 &=3a^2 + (2a)^2 = 7a^2 &&|\,\sqrt{}\\ f &= a\sqrt 7\end{aligned}$$Gruß Werner