Aufgabe:
2y´´+8y´-10y=3e^(4x)
Problem/Ansatz:
Hallo,
da ich keine Lösung für die folgende Aufgabe habe, würde ich mich freuen wenn mir jemad meine Lösung bestätigen könnte.
Oder vieleicht bin ich auch komplett am Thema vorbeigelaufen..?
Vor allem bei dem partikulären Teil bin ich mir unsicher.
Vielen Dank schonmal.
Grus Frost
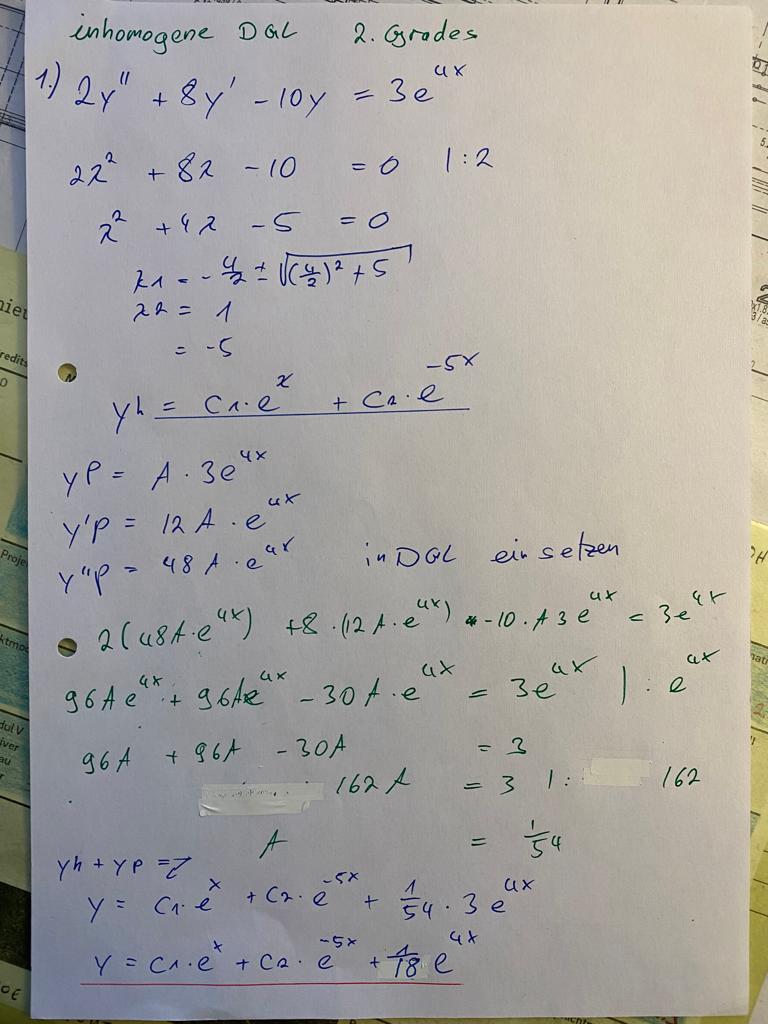
Text erkannt:
inhomogene DGL 2.Grades
1.) \( 2 y^{\prime \prime}+8 y^{\prime}-10 y=3 e^{4 x} \)
\( 2 \lambda^{2}+8 \lambda-10=0 \quad 1: 2 \)
\( \lambda^{2}+4 \lambda-5=0 \)
\( k_{1}=-\frac{4}{2} \pm \sqrt{\left(\frac{4}{2}\right)^{2}+5} \)
\( \lambda_{2}=1 \)
\( =-5 \)
\( y^{h}=c_{1} \cdot e^{x}+c_{1} \cdot e^{-5 x} \)
\( y^{P}=A \cdot 3 e^{4 x} \)
\( y^{\prime} P=12 A \cdot e^{u x} \)
\( y^{\prime \prime} p=48 A \cdot e^{4 x} \) inDGL einsetzen
\( \theta 2\left(48 A \cdot e^{4 x}\right)+8 \cdot\left(12 A \cdot e^{4 x}\right) 4-10 \cdot A 3 e^{4 x}=3 e^{4 x} \)
\( 96 A e^{4 x}+96 A e^{4 x}-30 t \cdot e^{4 x}=3 e^{4 x} \mid: e^{4 x} \)
\( 96 A+96 t-30 A=3 \)
\( y^{h+y p}=z \quad A \quad=\frac{1}{54} \)
\( y=c_{1} \cdot e^{x}+c_{2} \cdot e^{-5 x}+\frac{1}{54} \cdot 3 e^{u x} \)
\( y=c_{1} \cdot e^{x}+c_{2} \cdot e^{-5 x}+\frac{1}{18} e^{4 x} \)