Bei welcher Distanz haben 82% der Schuhbesitzer neue Schuhe gekauft?

Question

Aufgabe:

Suppose that your running shoes wear out with a mean of 610 km and a standard derivation of 88 km. If you decide to get a new pair when 82% of people would replace their shoes. What distance should you replace your shoes?

Problem/Ansatz:

… Der Erwartungswert ist 610 und die Standardabweichung 88. Wie kommt man jetzt auf die Zahl bei der 82% ihre Schuhe gewechselt haben?

Answer 1

P(X ≤ x) = NORMAL((x - 610)/88) = 0.82 --> x = 690.6 km

Du wechselst Deine Schuhe nach ca. 690.6 km

Skizze

Comments

Wie kommt man auf x = 690.6?

Varianz ist ja Standarbweichung^2.

---

Wie kommt man auf x = 690.6?

Die Gleichung die ich aufgestellt habe, wird nach x aufgelöst.

NORMAL((x - 610)/88) = 0.82

oder auch

Φ((x - 610)/88) = 0.82
(x - 610)/88 = Φ^{-1}(0.82)
x - 610 = 88·Φ^{-1}(0.82)
x = 610 + 88·Φ^{-1}(0.82)

Dabei kann die inverse Standardnormalverteilung in einer Tabelle abgelesen werden oder mit den TR berechnet werden.

---

Wo, auf welcher Seite kann man die Tabelle ablesen?

---

Du hast doch das Tafelwerk. Oder nicht? Ansonsten

https://www.google.de/search?q=standardnormalverteilung+tabelle

---

Meinen Sie folgende Tabelle für den "z-Wert"?

http://eswf.uni-koeln.de/glossar/zvert.htm

Oder ist hier wieder der p-Wert oder gar ein völlig anderer Wert gesucht?

---

Die Tabelle ist schon richtig.

---

Ich habe "inverse standardnormalverteilung tabelle" gegoogelt und auf den ersten Link geklickt.

Also falls das falsch sein sollte ist dein "let me google that for you" Link äußerst peinlich.

---

Also falls das falsch sein sollte ist dein "let me google that for you" Link äußerst peinlich.

Ich wusste halt nicht ob du google benutzen kannst. Wenn ja braucht man ja nicht nachfragen.

---

Die Tabelle ist schon richtig.

Und wo steht jetzt Mü = 610?

---

Und wo steht jetzt Mü = 610?

In der Aufgabe

Suppose that your running shoes wear out with a mean of 610 km and a standard derivation of 88 km. If you decide to get a new pair when 82% of people would replace their shoes. What distance should you replace your shoes?

---

"Die inverse Standardnormalverteilung kann in einer Tabelle abgelesen werden"

Das ist aber nicht ganz richtig.

Für x = 690.6, wie auch immer du auf diesen Wert gekommen bist (wahrscheinlich durch ein Programm) kommt (690.6-610)/88 = 0.91590909090909 raus.

In der Tabelle gibt es aber keine 0.9159. Der nächste Wert wäre 0.92 mit 0,8212. Gesucht ist aber ein Prozentwert von 82. Zeig mir bitte mal eine vernünftige Lösungsmethode mit der man den genauen Wert von x ablesen kann.

---

x = 610 + 88·Φ^{-1}(0.82)

Du liest den Wert für z in der Standardnormalverteilungstabelle ab

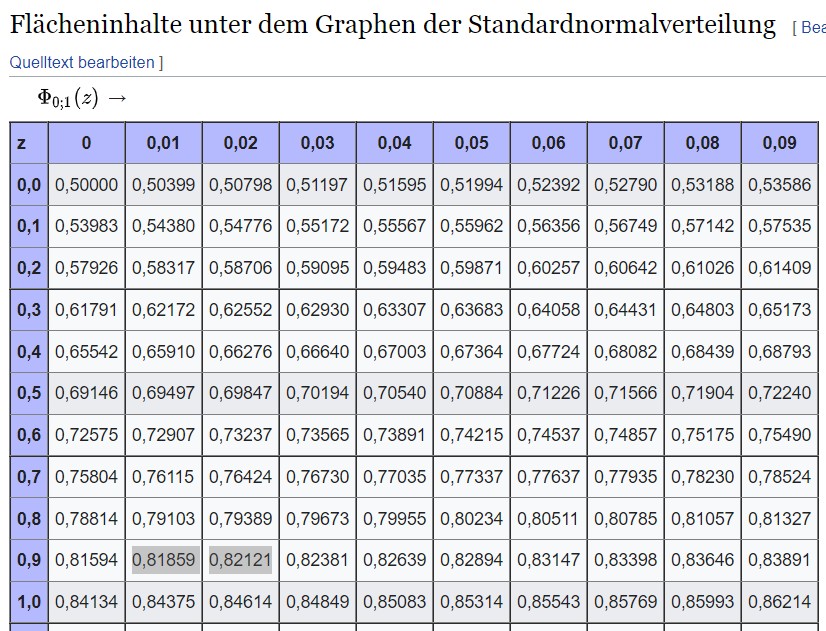
Du kommst auf etwas zwischen 0.91 und 0.92. Entweder näherst du jetzt dazwischen linear oder nimmst z.B. 0.915

Damit gehst du zurück in die Rechnung

x = 610 + 88·0.915 = 690.52

Mit einer linearen Näherung oder einem TR geht es noch etwas genauer.

---

Lineare Näherung

(0.92 - 0.91)/(0.82121 - 0.81859)·(0.82 - 0.81859) + 0.91 = 0.9153816793

x = 610 + 88·0.9153816793 = 690.5535877

Wir mussten das früher noch mit linearer Näherung machen. heutzutage brauchen die Schüler nur noch den nächsten Wert nehmen oder sie dürfen den TR benutzen.

Der TR kommt auf 0.9153645453. Intern rechnet er glaube ich noch ein oder 2 stellen mehr.

---

Der TR

Der TR ist lustig. Ich brauche die genaue Bezeichnung für das Modell. Geht das mit dem Taschenrechner aus deinem Profilbild? (CASIO fx 991DE X ClassWiz)

---

Ich bevorzuge den Casio geht aber auch mit Texas Instruments oder jedem anderen wissenschaftlichen Rechner.

Der CASIO fx 991DE X ClassWiz ist das Topmodell welches noch gerade im normalen Hamburger Abitur zugelassen ist. Deshalb empfehle ich den Casio.

---

Dann verrat mir bitte noch, wie man mit dem Casio auf 0.9153645453 kommt.

Menü, Sieben und dann?

---

Menü 7 3 0.82 = 1 = 0 =

xInv = 0.915...

---

Danke, aber was hat das jetzt genau mit einer "Fläche" zu tun?

---

Danke, aber was hat das jetzt genau mit einer "Fläche" zu tun?

Ist jetzt nicht dein erst oder? Schau mal folgendes Bild an

Ja. Was könnte das Wort Fläche wohl in dem Zusammenhang bedeuten. Ah vielleicht das es ein Integral ist was die Fläche zwischen dem Graphen und der x-Achse berechnet. Aber nur so eine Idee.

---

Mit welcher Seite kann man diese Fläche denn darstellen?

---

Und was bedeutet die 0.915 im Bezug auf die Fläche?
Die 0.82 bedeutet ja, dass 82% der gesamten Fläche von links nach rechts eingefärbt ist.

---

Ist jetzt nicht dein erst oder?

Aber interessant wie du verlangst, dass man um 3:00 nachts (die Uhrzeit wo das Gehirn am aktivsten ist), direkt darauf kommt, wofür die Fläche bei der inversen Normalverteilung im Casio steht. Ich stelle mal die Nullhypothese auf, dass weniger als 50% das wissen.

---

Ich stelle mal die Nullhypothese auf, dass weniger als 50% das wissen.

Die Nullhypothese würde dann sein, dass mehr.