Aloha :)
Wir füllen das Mengendiagramm schrittweise zusammen aus:
$$(\mathrm a)\;\; (A\cap B)\setminus C=\emptyset$$$$(\mathrm d)\;\; (A\cap B\cap C)=\{4\}$$
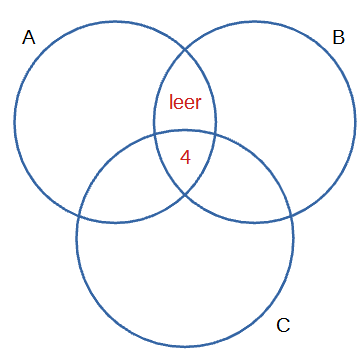
Die \(\red{\mathrm{rote}}\) Schrift soll bedeuten, dass diese Flächen fertig sind, da kommt nichts mehr dazu.
$$(\mathrm b)\;\; A\setminus C=\{5;10\}$$$$(\mathrm e)\;\; B\setminus(A\cup C)=\{8\}$$$$(\mathrm g)\;\; C\setminus(A\cup B)=\{11\}$$
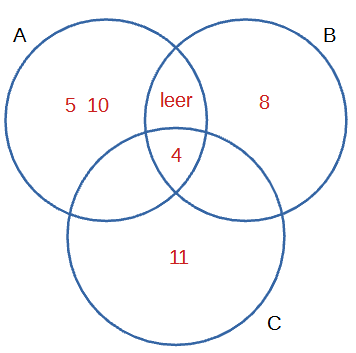
$$(\mathrm c)\;\; (A\cap C)\setminus B=\{3;9\}$$$$(\mathrm f)\;\; B\cap(A\cup C)=\{1;2;4;6;7\}$$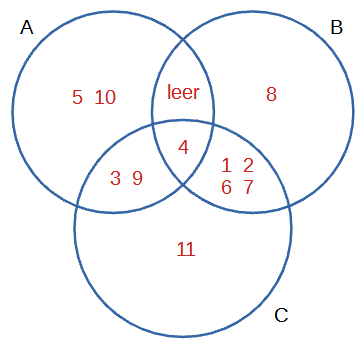
Deine Lösung stimmt fast.
Du hast bei der Menge C nur die Teilmenge mit \(\{1;2;6;7\}\) übersehen.