Zunächst eine Skizze:
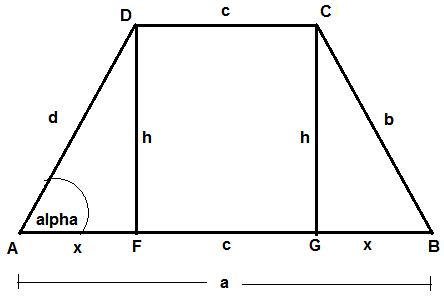
In einem gleichschenkligen Trapez gilt einerseits b = d ( die Schenkel sind gleich lang) und andererseits, wie man an der Skizze erkennen kann,
c = a - 2 x
wobei x die Strecke zwischen den Punkten A und F bzw. G und B ist.
Da AFD ein rechtwinkliges Dreieck mit x und h als Katheten sowie d als Hypotenuse ist, gilt:
h / d = sin (alpha )
Mit h = 16 und d = b = 19 ergibt sich
<=> alpha = arcsin ( h / d ) = arcsin ( 16 / 19 ) ≈ 57,36 °
Damit kann nun kann auch x berechnet werden:
x / d = cos ( alpha )
<=> x = d * cos ( alpha ) = 19 * cos ( 57,36 ° ) ≈ 10,25 cm
Damit ergibt sich für die Länge der Seite c:
c = a - 2 x = 23 - 20,5 = 2,5 cm
und für den Flächeninhalt A des Trapezes:
A = h * ( a + c ) / 2 = 16 * ( 23 + 2,5 ) / 2 = 204 cm 2
x / d = cos ( alpha )
<=> x = d * cos ( alpha )
Mit d = b = 19 cm und mit alpha =