Hallo,
mein erster Gedanke war, dass das nicht geht. Du kannst mit drei Kreisen ein Ebene nur in 8 statt 10 Bereiche unterteilen, Der Trick besteht darin, dass diese Ebene endlich ist. Berühen bzw. schneiden die drei Kreise den äußeren Kreis kommt man auf 10 Bereiche.
Hier eine Möglichkeit, wenn man davon ausgeht, dass jede Katze 'punktförmig' ist und ihre Position sich in der Sitzfläche befindet:
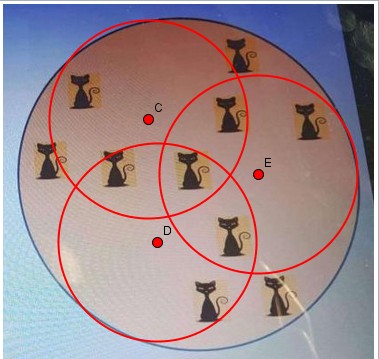
Die Punkte sind nur dazu da die Position der Kreise zu verändern.
Gruß Werner