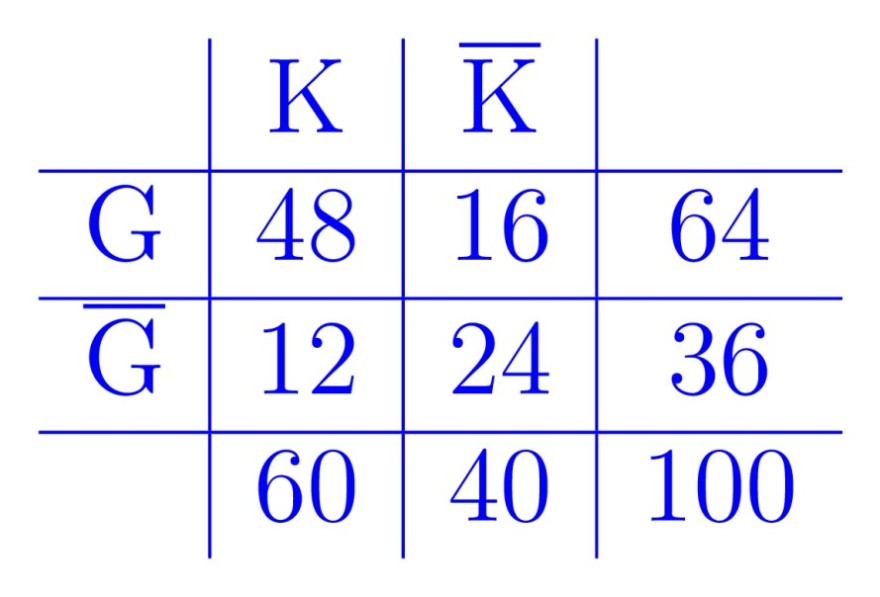
Bei bedingten Wahrscheinlichkeiten empfiehlt es sich zunächst immer eine Vierfeldertafel zu zeichnen:
P(K) = Die Wahrscheinlichkeit, dass der Kapitän in guter Form ist.
P(G) = Die Wahrscheinlichkeit, dass die Mannschaft ein Spiel gewinnt.
Auf die 48 kommst du, wenn du 0,8 * 0,6 rechnest und dann mal 100.
Auf die 12 kommst du, weil 48 zusammen mit 12 die 60 ergeben muss.
Warum 0.8 mal 0.6?
Weil die Mannschaft zu 80% gewinnt und der Kapitän in 60% von diesen Spielen in guter Form ist.
Auf die 16 kommst du, wenn du 0,4 * 0.4 rechnest und dann mal 100.
Auf die 24 kommst du, weil 16 zusammen mit 24 die 40 ergeben muss.
Warum 0.4 mal 0.4?
Weil die Mannschaft zu 40% verliert und der Kapitän in 40% von diesen Spielen nicht in guter Form ist.
Bei a) musst du einfach schauen, was ganz rechts in der Spalte von G steht. Das wäre hier 64%.
Bei b) ist es bisschen schwieriger. Da muss du erstmal schauen wie viele Spiele die Mannschaft, mit einem Kapitän, der in guter Form ist verliert (12) und das dann anschließend noch durch die gesamte Anzahl der verlorenen Spiele teilen (33).
Das nennt sich dann bedingte Wahrscheinlichkeit, hier die Formel dazu:
$$\text{P}(\text{K}|\overline{\text{G}})=\frac{\text{P}(\text{K}\cap\overline{\text{G}})}{\text{K}(\overline{\text{G}})}=\frac{12}{36}=\frac{1}{3}=0.333$$
a) Die Mannschaft gewinnt mit einer Wahrscheinlichkeit von 64% das Spiel.
b) Falls die Mannschaft ein Spiel verliert, ist der Kapitän nur zu 33.3% in guter Form.