Bestimmen Sie die Anzahl der Fernseher, die mindestens produziert werden müssen, ....

Question

Aufgabe:

Eine Firma stellt Fernseher her, von denen 3% Ausschuss sind.

Bestimmen Sie die Anzahl der Fernseher, die mindestens produziert werden müssen, damit mit 90% iger Wahrscheinlichkeit zumindest ein defekter dabei ist.

Answer 1

Bestimmen Sie die Anzahl der Fernseher, die mindestens produziert werden müssen, damit mit einer Wahrscheinlichkeit von mindestens 90% mindestens ein defekter dabei ist.

Es handelt es sich um eine 3 mal mindestens Aufgabe.

n = gesucht
p = 0.03

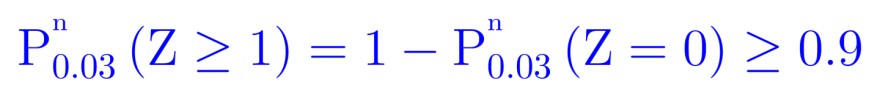
$$=1-\underbrace{\binom{n}{0}\cdot 0.03^{\,0}}_1\cdot0.97^{\text{n}}\geq0.9\\1-0.97^{\text{n}}\geq0.9\\\text{n}\geq\frac{\ln(1-0.9)}{\ln(0.97)}\\\text{n}\geq75.6$$ (Hier immer auf die nächste höhere Zahl aufrunden.)

A: Es müssen mindestens 76 Fernseher produziert werden, damit mit einer Wahrscheinlichkeit von mindestens 90% mindestens ein defekter dabei ist.

Answer 2

von denen 3% Ausschuss sind.

Dann ist mit einer Wahrscheinlichkeit von (1 - 3%)ⁿ kein einziger von n produzierten Fernsehern kaputt.

Gegenereignis.

Answer 3

Eine Firma stellt Fernseher her, von denen 3% Ausschuss sind. Bestimmen Sie die Anzahl der Fernseher, die mindestens produziert werden müssen, damit mit 90% iger Wahrscheinlichkeit zumindest ein defekter dabei ist.

P(mind einer defekt) = 1 - P(keiner defekt) = 1 - (1 - 0.03)^n ≥ 0.9 --> n ≥ 76 Fernseher