Aufgabe:
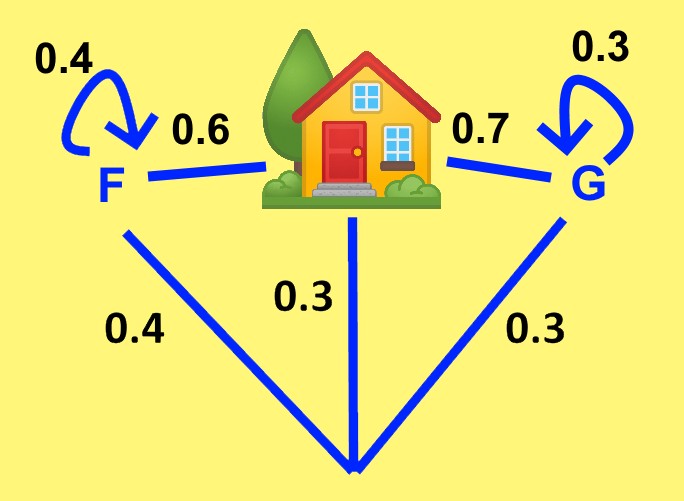
Ein Student ist am Wochenende nach der Uni zunächst in der Stadt. Er hat die Wahl, mit einer Wahrscheinlichkeit von 0,4 auf ein Festival zu gehen und mit 0,3 in ein Gaming Café. (Er wird aber garantiert im Laufe der Zeit nach Hause zurückzukehren).
Wenn er auf dem Festival ist, nimmt er sich 2 Stunden Zeit und entscheidet dann, ob er weiterhin auf dem Festival bleibt oder ob er nach Hause zurückkehrt. (Er kann auch weiterhin, wie in einem rekursiven Prozess entscheiden, auf dem Festival zu bleiben).
In ähnlicher Weise entscheidet er, nachdem er 3 Stunden in dem Gaming Café war, entweder dort zu bleiben oder nach Hause zurückzukehren. (Er kann weiterhin wie in einem rekursiven Prozess entscheiden, in dem Café zu bleiben). In allen Fällen dauert der Heimweg 1 Stunde.
Wie viele Stunden war der Student voraussichtlich außer Haus?
Problem/Ansatz:
Skizze:
E(X) = 0.3 * 1 + ... ?