Vergleich zweier eingeschriebener Figuren

Question

Aufgabe:

Vergleich zweier Aufgaben im Bereich maximaler/minimaler Flächeninhalt einer eingeschriebenen Figur

Problem/Ansatz:

Ich vergleiche gerade zwei Aufgaben aus diesem Bereich. Und ich frage mich wieso die eine Aufgabe eigentlich einen Minimalwert besitzt für den Flächeninhalt und die andere einen Maximalwert. Wann eine quadratische Funktion ein Maximum und Minimum besitzt weiß ich natürlich. Aber ich frage mich wieso ist es so wie es ist. Im Endeffekt sind die beiden Aufgaben sich sehr ähnlich. Einmal soll einem Quadrat ein Trapez mit maximalen Flächeninhalt eingeschrieben werden und einmal einem Rechteck ein Dreieck mit maximalen Flächeninhalt.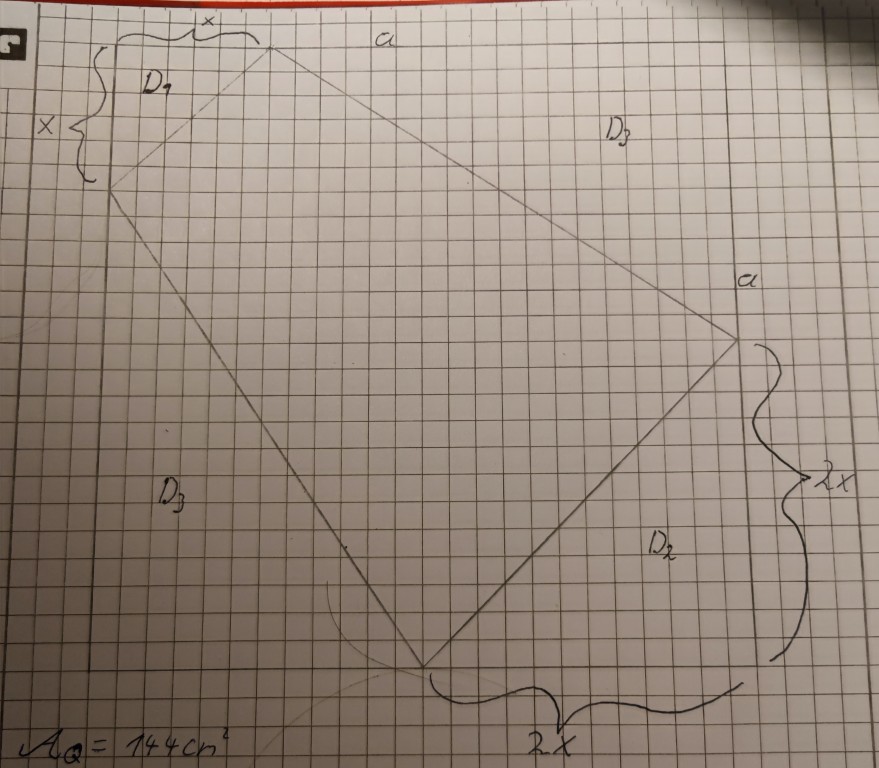

Text erkannt:

\( \left.\begin{array}{l}D_{1} x_{0}^{x}+D_{3}\end{array}\right\} \)

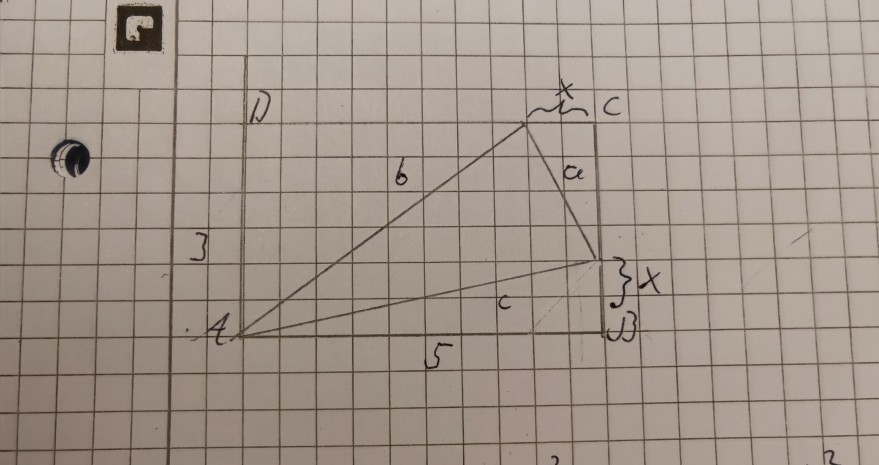
Die Funktionen lauten im Übrigen:
A(R) = 0.5×(x-2.5)^2+4.375
A(T)=-4.5×(x-4)^2+72

Rechteck mit den Seitenlängen 3 und 5 cm. Quadrat mit der Seitenlänge 12cm

Answer 1

Tia, an was liegt das?

Wenn man die Funktionsgleichung nicht anschaut (Parabeln haben entweder ein TOP oder ein TIP)/oder nicht hat, dann kann man feststellen daß

es unterschiedliche Startbedingungen gibt k=x

x=0 ==> V_Trapez = 0, V_Dreieck = max

x>0 ==> V_Trapez wird größer, V_Dreieck wird kleiner und irgendwann kippt das Wachstum

Comments

Dankeschön! Ich werde es mir noch einmal anschauen

Answer 2

A(R) = 0.5×(x-2.5)^2+4.375

Der Funktionsterm bildet doch hier eine nach oben geöffnete Parabel welche natürlich nur ein Minimum und Randmaxima hat.

A(T) = -4.5×(x-4)^2+72

Der Funktionsterm bildet doch hier eine nach unten geöffnete Parabel welche natürlich nur ein Maximum und Randminima hat.

Die Funktionsterme selber habe ich nicht geprüft sondern einfach übernommen.

Comments

Danke für die Antwort. Ja soweit ist das vom Verständnis her ja auch kein Problem für mich. Mich interessiert eher wieso es ist wie es ist. Im Endeffekt sind es ja beides geometrische Figuren in ein Vieleck eingeschrieben. Wieso hat die eine Figur aber eine Maximum und die andere ein Minimum, wenn doch der Sachverhalt so gut wie der selbe ist?

---

Grundsätzlich könntest du dir mal ein paar Trapeze oder Dreiecke wie gefordert einzeichnen. Zeichne auch immer die Figuren ein wenn x die Grenzen des Definitionsbereiches erreicht. Für x = 0 würde die Fläche des Trapezes auch null werden. Wo bei du jetzt schon siehst das dann eine Funktion verkehrt aufgestellt ist.

---

Müssten soweit richtig sein die Funktionen. für x=0 ist die Fläche des Trapezes laut Funktion auch null.

---

Ja das mit den Skizzen habe ich schon gemacht. Ich werde es mir nochmal anschauen.

---

Oh sorry. Das war mein Fehler.

Wenn ein Randwert 0 ist dann müsste, wenn es ein Extremwert gibt dieser dann auch ein Hochpunkt sein. Zumindest wenn wir mal positive Funktionswerte für Flächen etc. voraussetzen.