Verhältnis Flächenstück das durch die Schnittpunkte der Funktionsgraphen verlaufenden Geraden geteilt

Question

Aufgabe:

Berechne den Inhalt des Flächenstücks, das von den Graphen der Funktionen f und g begrenzt wird. In welchem Verhältnis wird dieses Flächenstück von der durch die Schnittpunkte der beiden Funktionsgraphen verlaufenden Geraden geteilt f(x) = x^2-2x+1, g(x) = -2x^2+10x+16

Problem/Ansatz:

Es ist für uns ein komplett neues Themengebiet und wir sind mit so gut wie keiner Erklärung uns selbst überlassen. Wir bitten daher um Hilfe, damit wir es verstehen.

Answer 1

Hallo,

berechne zuerst Schnittpunkte der beiden Funktionen, indem du die Funktionsterme gleichsetzt.

\(x^2-2x+1=-2x^2+10x+16\\ 3x^2-12x-15=0\\ x^2-4x-5=0\\ x_{1,2}=2\pm\sqrt{9}\\ x_1=-1\quad x_2=5\\\)

Berechne die Differenzfunktion h(x) = g(x) - f(x) = 2. Zeile oben und bilde davon die Stammfunktion.

\(h(x)=3x^2-12x-15\qquad H(x)=x^3-6x^2-15x\)

Berechne das Integral zwischen den Schnittpunkten.

\( \begin{aligned} & \int \limits_{-1}^{5}\left(3 x^{2}-12 x-15\right) d x \\=& {\left[x^{3}-6 x^{2}-15 x\right]_{-1}^{5} } \\=&\left|5^{3}-6 \cdot 25-75-(-1-6+15)\right| \\=&|-108|=108 \end{aligned} \)

Stelle die Gleichung der Geraden durch die Schnittpunkte auf.

y = 2x + 6

Berechne wie oben den Flächeninhalt zwischen f und der Geraden.

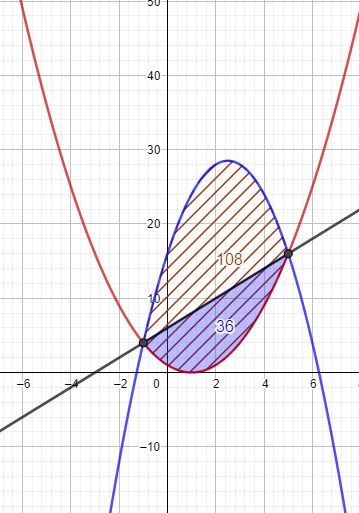
Gruß, Silvia