Spiegelung an einer horizontalen Geraden

Question

Aufgabe:

Gegeben ist die Funktion f mit der Gleichung f(x) = -2xhoch2 + 4x + 16

Der Graph von f wird an der Y- Achse und anschließend an der Geraden g(x)= 3 gespiegelt. Geben die die Funktionsgleichung der so entstandenen Parabel h an .

Problem/Ansatz:

Ich verstehe diese Aufgabe leider nicht . Ich habe viel probiert aber ich weiß nicht wie man es berechnet. Wäre sehr lieb falls mir jemand helfen könnte, weil ich morgen eine Klausur schreibe .

Answer 1

Schaffst du es grafisch zu spiegeln oder schaffst du es sogar nur den Scheitelpunkt zu spiegeln. Das hilft dir schon, um die gesamte Funktion zu spiegeln.

y1 = - 2·x^2 + 4·x + 16

Spiegeln an der y-Achse

y2 = - 2·(- x)^2 + 4·(- x) + 16
y2 = - 2·x^2 - 4·x + 16

Spiegeln an der Geraden y = 3

y3 = - (- 2·x^2 - 4·x + 16 - 3) + 3
y3 = 2·x^2 + 4·x - 10

Answer 2

Bei Spiegelung an der y-Achse musst du x durch -x ersetzen.

Die Spiegelung an g erscheint etwas aufwendiger zu sein.

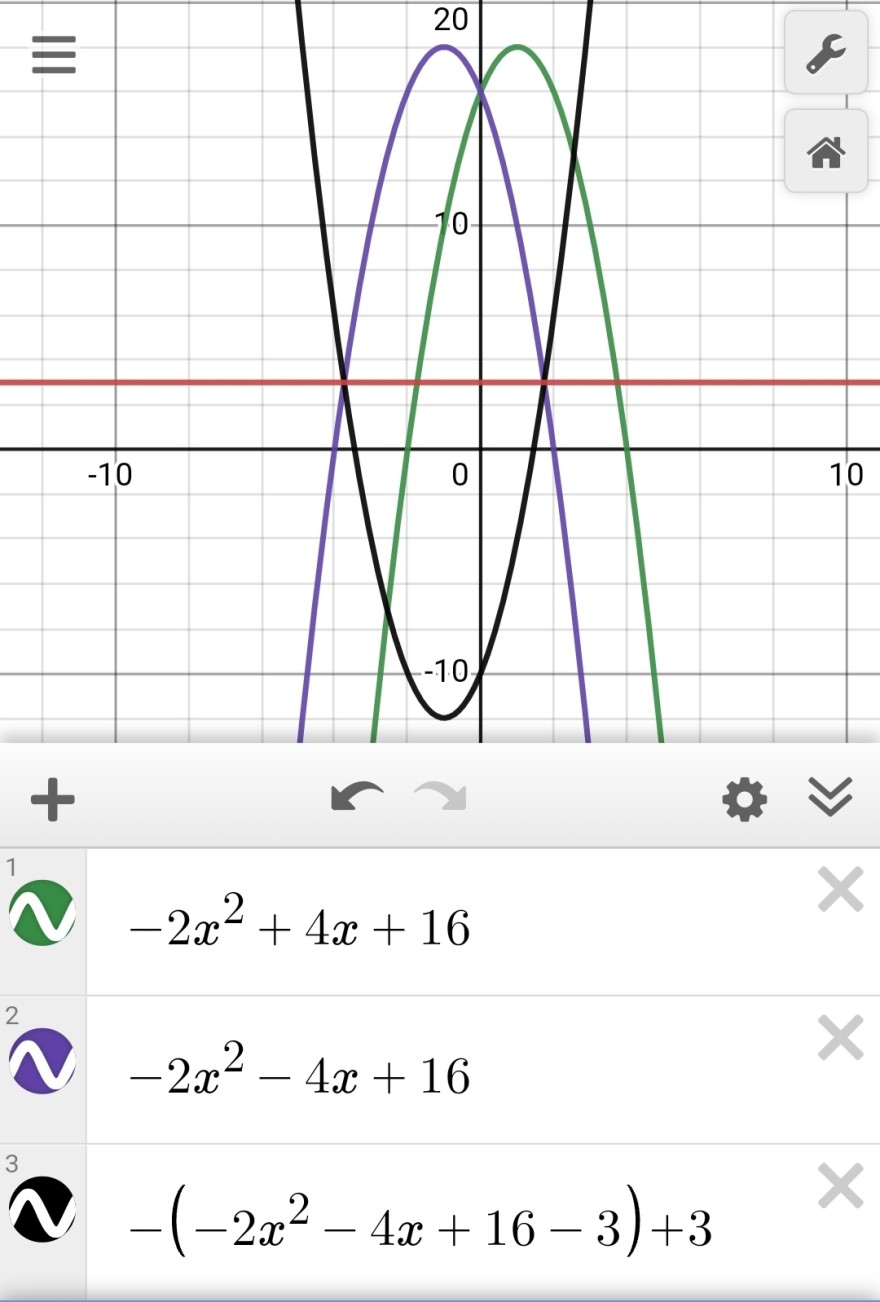
So geht es rechnerisch einfach.

Aus -2x²-4x machst du 2x²+4x.

Dann überlegst du, bei welcher Zahl die +16 landet. Von 16 bis 3 ist es -13. Den gleichen Schritt noch einmal ergibt 3-13=10.

--> 2x²+4x-10

:-)