Warum ist die folgende Menge nicht leer? (Schnitt/Vereinigung von Teilmengen)

Question

Warum ist die folgende Menge nicht leer?

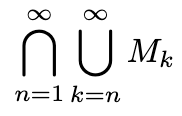
Wenn ich das richtig verstehe ist die Vereinigung von allen Mk ja einfach M, und dann schneidet man Teilmengen von M mit M? Aber der Schnitt aller Teilmengen ist ja nicht zwangsläufig nicht leer, wieso ist das hier anders?

Answer 1

Die Menge ist nicht leer, weil

        \( \bigcap\limits_{n=1}^{\infty} \bigcup\limits_{k=n}^{\infty} M_{k} = \{n\in \{1, \ldots, N\} |\ \varphi(n) = \infty\}\)

ist.

Comments

Ich verstehe leider die Menge nicht ganz - was genau macht das phi?

---

Sag mir, was M ist und was die \(M_k\) sind, dann verrate ich dir was das \(\varphi\) ist.

ist die Vereinigung von allen Mk ja einfach M

Das kann man aus der Bezeichnung \(M_k\) nicht schlussfolgern. Und mehr als deren Name hast du über die Mengen nicht offenbart.