Question

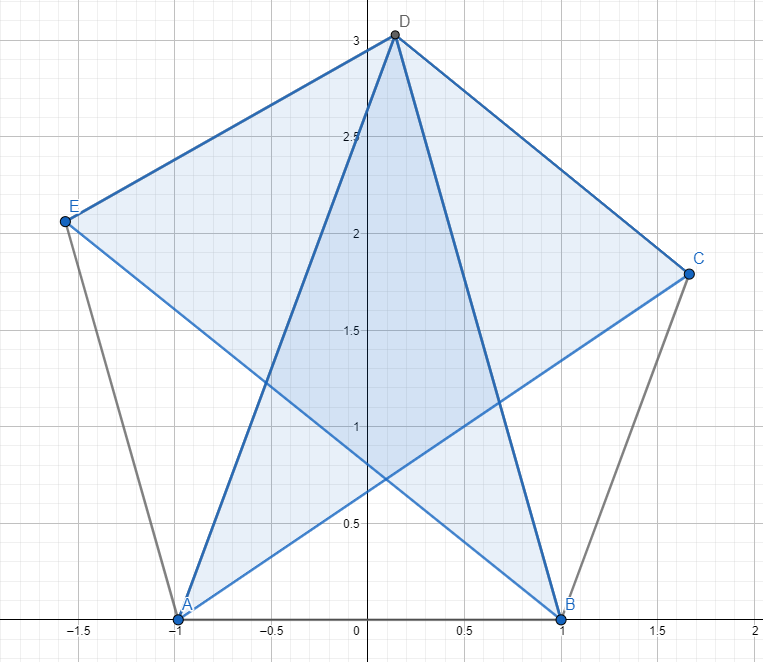
Wie kann ich beweisen, dass die Fläche des Dreiecks ACD gleich der Fläche des Dreiecks BDE ist, wenn dies ein konvexes Fünfeck ist?

Mein Ansatz war, zu zeigen, dass die Winkel ACB und CAD gleich sind, sowie die Winkel AEB und DBE gleich sind (weil sie Wechselwinkel sind): Aber nun komme ich nicht weiter.

Ich würde mich über schnelle Hilfe freuen

Comments

Deine Dreiecke in einem regelmäßigen 5-Eck sind nach dem Kongruenzsatz sss deckungsgleich und haben damit den gleichen Flächeninhalt.

---

Mein Fünfeck ist aber nicht regelmäßig, sondern nur konvex. Wie kann ich das dann beweisen?

---

Dann kannst du es nicht zeigen, weil es nicht gilt

---

Oh, entschuldigung, ich habe vergessen zu schreiben, dass AE parallel zu BD ist und AD parallel zu BC ist. Mein Fehler. Es wäre nett, wenn du jetzt nochmal danach gucken könntest.

---

Momentan nicht so aus dem Kopf, aber wir hatten diese Frage vor nicht allzu langer Zeit hier auf der Seite.

Wenn du den genauen Fragetext hast, dann könntest du danach suchen. In der Hoffnung die Leute stellen die Frage im Original.

---

Aktuelle Mathe-Olympiade...

---

Aktuelle Mathe-Olympiade...

Dachte ich auch zuerst. Die Aufgabe der Mathematik-Olympiade war aber tatsächlich etwas anders.

---

Beide Aufgaben lassen sich aber mit einer sehr ähnlichen (übrigens recht einfachen) Lösungsidee erledigen.

---

Das ist tatsächlich von der Mathe-Olympiade, aber ich musste die Aufgaben schon abgeben und wollte einfach mal gucken, wie weit ich komme. Und an dieser Stelle bin ich nicht weitergekommen.

---

Ich habe mir erlaubt den Hinweis von Gast hj2166 zu löschen, da er direkt zur Lösung führte.