Aufgabe:
In einer bestimmten Stadt haben 8 % der Männer über 60 Jahren Diabetes, aber nur 4 % der Männer im Alter
unter 60 haben die Krankheit. Wenn ein Mann tatsächlich Diabetes hat, hat der Arzt eine Wahrscheinlichkeit von 90 % richtig zu diagnostizieren. Wenn ein Mann die Krankheit nicht hat, hat der Arzt eine Wahrscheinlichkeit von 2 % falsch zu diagnostizieren. 20 % der Männer in dieser Stadt sind 60 oder älter. Finde die Wahrscheinlichkeit dafür, dass
(a) ein Mann über 60 Jahren ist und bei dem vom Arzt Diabetes diagnostiziert wurde.
(b) ein Mann tatsächlich an der Krankheit leidet, nachdem der Arzt bei ihm Diabetes diagnostiziert hat.
Problem/Ansatz:
Skizze: Doppelte Vierfeldertafel
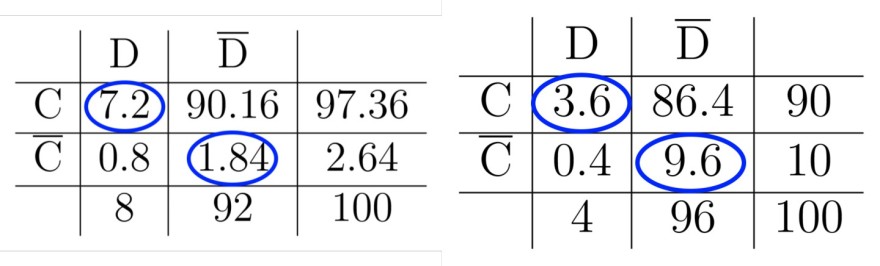
(die linke Tafel gilt für Männer über 60, rechte Tafel für Männer unter 60)
a) Ich addiere die blau umkreisten Felder und multipliziere anschließend mit 0,2 da es ja nur 20% Männer über 60 gibt: (7.2+1.84) * 0.2 = 1.808 [%]
Das soll richtig sein.
b) Ich addiere die Menge der wirklich Kranken und teile diese Menge durch alle vier umkreisten Felder: (7.2 * 0.2 + 3.8 * 0.8) / ((7.2+1.84) * 0.2 + (3.6+9.6) * 0.8) = 0.36222
Es soll aber ein Wert von ungefähr 60-70% rauskommen bei b, wo liegt der Fehler?