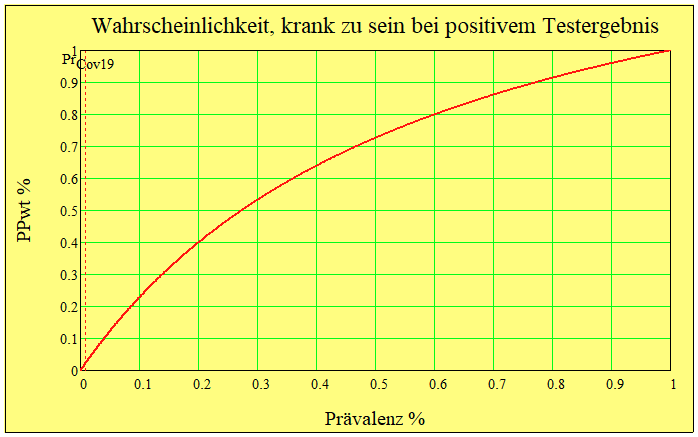
Das ist doch eine schöne Aufgabe, kann man gleich auf die heutige Situation mit Covid19 anwenden.
Gesucht ist also die positiv prädikative Wahrscheinlichkeit \( = \text{PPwt} \)des Testergebnisses. Die berechnet sich wie folgt
$$ \text{PPwt} = \frac{ Pr \cdot dSe }{ Pr \cdot dSe + (1-Pr) (1-dSp) } $$ wobei
\( dSe = \text{Sensitivität} \)
\( dSp = \text{Spezifität} \)
\( Pr = \text{Prävalenz} \)
ist.
Mit Deinen Zahlen kommt dann \( \text{PPwt} = 2.6 \% \) raus. Das heisst nur mit einer 2.6-prozentigen Wahrscheinlichkeit ist das Testergebniss richtig. Allerding ist die negative prädiktive Wahrscheinlichkeit 99.6%. Das heisst, ein negatives Testergebnis ist sehr zuverlässig und ein positives sehr unzuverlässig.
Das wird nur besser, wenn die Prävalenz höher wird.