1) Wie groß ist die Bahngeschwindigkeit der Erddrehung?

Question

Aufgabe: 1) Wie groß ist die Bahngeschwindigkeit v der Erddrehung am Äquator?
2) Welche Zentripetalbeschleunigung a erfährt ein Körper durch die Erddrehung
am Äquator? Wie groß ist diese im Verhältnis zur Erdbeschleunigung g?
3) Wie groß sind v sowie a für die geographische Breite φ =47,26◦?

Problem/Ansatz: Bei nummer 1 hab ich es so versucht v= 2pi*6378km/24h mein Ergebnis stimmt aber nicht mit der Lösung überein.

2 und 3 fehlt mir der Ansatz

Comments

zu 1) wie sieht dein Ergebnis aus?

zu 2) hast du eine Formel für Zentrifugal- bzw. Zentripetalkraft?

zu 3) zeichne ein Dreieck und überlege, wir groß der Abstand zur Erdachse ist.

---

Nummer 1 hat sich alles geregelt.

Bei der Nummer zwei hätte ich den Ansatz w^2*r, als formel...nur wenn ich alles einsetze kommt 0,0337 m/s^2 raus. Das ist aber die falsche Lösung, glaub ich halt.

Ich hab ein Dreieck gezeichent. Der Abstand zur Erdachse ist ja der Radius oder? Ich komm einfach auf keine Lösung

---

zu 2) du hast richtig gerechnet, bravo!!!

zu 3) der relevante Radius ist 4329 km (errechnet aus 6378 km · cos(47,26°). Das ergibt eine Bahngeschwindigkeit von ≈ 1088 km/h ≈ 302 m/s. a_Z = 0,0211 m/s² an dieser Stelle.

Answer 1

zu 1)

wenn für eine Erdumdrehung 24 h angenommen werden, ist die Bahngeschwindigkeit v_B ≈ 1670 km/h ≈ 464 m/s.

die Erde braucht tatsächlich nur ≈ 23,93 h für eine Umdrehung. Rechnet man damit, ist die Bahngeschwindigkeit v_B ≈ 1674 km/h ≈ 465 m/s.

zu 2)

a_Z=\( \frac{v^{2}}{r} \)  nehmen wir das v für 24 h pro Erdumdrehung. Dann ist a_Z=0,0337 m/s²

zu 3)

der Radius zur Erdachse ist r_Äquator·cos(φ). Ich habe das als grüne Linie eingezeichnet.

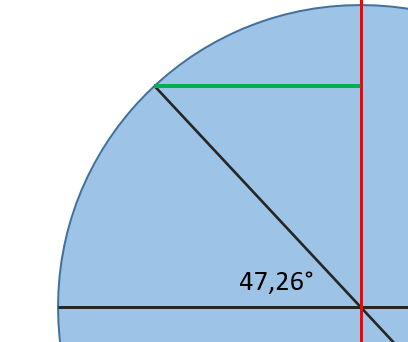
Berechne diesen Radius und rechne damit die Bahngeschwindigkeit und Zentripedalkraft aus wie in Aufgabe 1) und 2) aus.

Anmwerkungen:

Ergebnisse gebe ich mit einer Genauigkeit von drei Ziffern an, ausser wenn die erste Ziffer eine 1 ist. Das hat mir ein kluger Professor vor langer Zeit beigebracht. Die Rechnungen selbst führe ich mit hoher Genauigkeit durch.

Der Erdradius nimmt zum Nordpol hin leicht ab, das wurde bei Frage 3) nicht berücksichtigt.

Comments

Vielen Dank! Du hast mir wirklich sehr weiter geholfen:)