Question

Kann man g(x) = f(3-x) als g(x) = f(-x+3) darstellen?

Hintergrund der Frage: Gegeben sei folgender Graph:

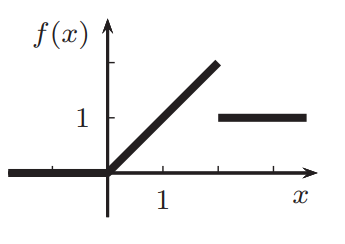
Und ich soll nun den Funktionsgraphen zu g(x) = f(3-x) zeichnen.

Die Lösung suggeriert mir, zunächst um 3 nach links zu verschieben und dann erst an der y-Achse zu spiegeln.

Allerdings wollte ich zuerst spiegeln und dann verschieben = g(x) = f(-x+3)

Da kommt aber was anderes raus

Comments

Das finde ich aber seltsam; denn -x+3=3-x.

---

Da kommt aber was anderes raus

Logisch, denn  zuerst spiegeln und dann verschieben führt zuerst auf h₁(x) = f(-x) und dann auf h₂(x) = h₁(x+3) = f(-(x+3)) = f(-x-3) ≠ g(x)

---

Ich verstehe das immer noch nicht!
Was war mein Fehler und WIE soll ich das in der Klausur machen?

Wieso sollte man bei g(x) = f(3-x) um 3 nach rechts verschieben, obwohl unser a hier positiv ist, denn es gilt ja: f(x-a): Verschiebung des Fkt.graphen um a nach rechts

Answer 1

Ich empfehle den Faktor auszuklammern

g(x) = f(- x + 3) = f(- (x - 3))

Hier sieht man, dass der Graph zuerst an der y-Achse gespiegelt wird und dann um 3 nach rechts verschoben wird

Erinnere dich vielleicht an die allgemeine Sinusfunktion mit den Parametern a, b, c und d

y = a·SIN(b·(x + c)) + d

Comments

Ah ok, das mit der Ausklammerung hat mir jetzt doch ein bisschen weitergeholfen. Danke!

Answer 2

Es ist doch \(-x+3=3-x\), also auch
\(f(-x+3)=f(3-x)\).

Comments

Mein Beitrag ging am Problem vorbei, sorry.