Gaußschen Zahlenebenen komplexe Zahlen einzeichnen

Question

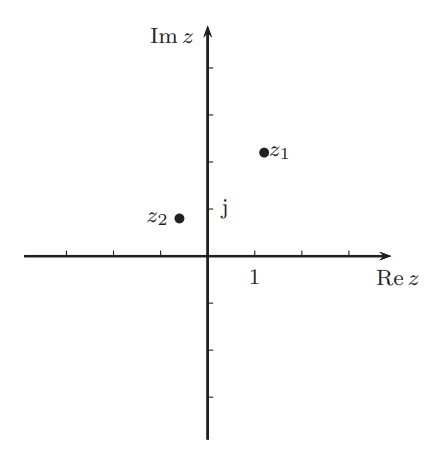
Auf der folgenden Gaußschen Zahlenebenen sind die beiden komplexen Zahlen z1 und z2 markiert.

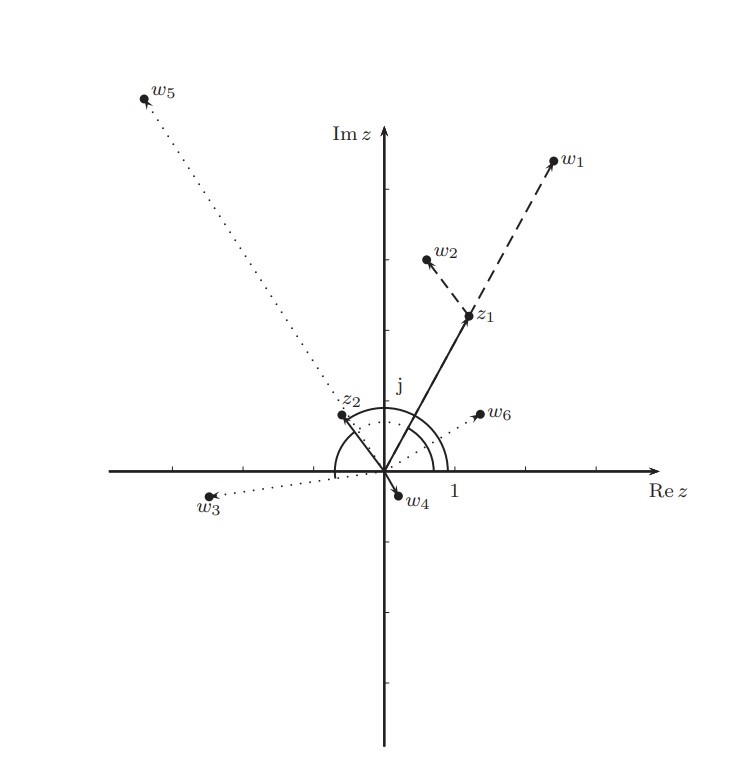
Nun soll ich drauf skizzieren, wo ungefähr die folgenden Zahlen liegen:

w4 = 1 / z1

ein w6 mit w6^2 = z1

Ich hab zwar die Lösungen, allerdings brauche ich eine Erklärung, wie genau man drauf kommt.
So sieht die Lösung aus:

Answer 1

Ich hab zwar die Lösungen, allerdings brauche ich eine Erklärung, wie genau man drauf kommt.

Ich habt sicher gelernt was mit Betrag und Winkel einer Komplexen Zahl passiert, wenn man die Wurzel zieht, wenn man quadriert oder wenn man komplexe Zahlen teilt.

Genau dieses Wissen ist jetzt von dir gefragt. Wenn du das Wissen nicht mehr parat hast solltest du im Skript nachsehen und oder dir vielleicht einen eigenen Merkzettel dafür anlegen.

Answer 2

Aloha :)

Wie betrachten den Kehrwert einer komplexen Zahl in Polardarstellung \(z=r\cdot e^{i\cdot\varphi}\):$$\frac1z=\frac{1}{r\cdot e^{i\cdot\varphi}}=\frac1r\cdot e^{-i\cdot\varphi}$$Von der Länge \(r\) des Vektors zum Punkt \(z_1\) wird also der Kehrwert genommen und der Winkel mit der \(x\)-Achse geht von \(\varphi\) in \((-\varphi)\) über, d.h. an der \(x\)-Achse gespiegelt. Das ergibt den Punkt \(w_4\).

Wir betrachten die Wurzel aus einer komplexen Zahl in Polardarstellung \(z=r\cdot e^{i\cdot\varphi}\):$$\sqrt{z}=\sqrt{r\cdot e^{i\cdot\varphi}}=\sqrt r\cdot \sqrt{e^{i\cdot\varphi}}=\sqrt r\cdot e^{i\cdot\frac12\varphi}$$Die Länge \(r\) des Vektors zum Punkt \(z_1\) wird also "gewurzelt" und der Winkel bezüglich der \(x\)-Achse wird halbiert. Das liefert den Punkt \(w_6\).