Im Prinzip soll ja hier die Aufgabe $$ x = Ax + b $$ mit \( A=\begin{pmatrix} 0 & -\frac{1}{2} & -\frac{1}{4} \\ -\frac{1}{2} & 0 & 0 \\ 0 & -\frac{1}{2} & 0 \end{pmatrix} \) und \( b=\begin{pmatrix} \frac{3}{4} \\ -2 \\ -\frac{1}{2} \end{pmatrix} \) gelöst werden.
Die Lösung ist $$ x = -(A-I)^{-1} b = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix} $$
Für die Iteration muss ein Startvektor gewählt werden, z.B. \( x_0 = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \)
Dann ergibt sich \( x_1 \) zu
$$ x_1 = A x_0 + b = \begin{pmatrix} 0 \\ -\frac{5}{2} \\ -1 \end{pmatrix} $$
Das muss jetzt iterativ weiter geführt werden. Das sieht dann z.B. so aus
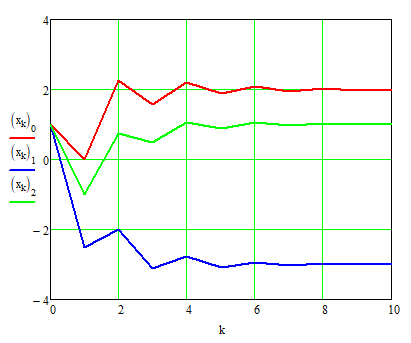
Wie man sieht konvergiert die Iteration gegen die richtige Lösung.
Um die Anzahl der Iterationen anzuschätzen gilt ja die Formel
$$ \| \tilde x - x_n \| \le \frac{L^n}{1-L} \| x_1 - x_0 \|| $$ wenn \( \tilde x \) die exakte Lösung ist. Und das soll kleiner \( \varepsilon = 10^{-14} \) sein.
Daraus folgt $$ n \ge \frac{ \ln \left( \frac{ 1-L }{ \| x_1 - x_0 \| } \varepsilon \right) } { \ln(L) } $$
wobei \( L \) die Lipschitzkonstante ist. Die Lipschitzkonstante ist hier die Matrixnorm.
Somit ist die Schätzung für die Anzahl der Iterationen vom Startvektor und von der Wahl der Matrixnorm abhängig.
Ich habe die Frobeniusnorm gewählt undkomme damit auf \( n \ge 346 \) Für z.B. die Zeilensummennorm bekommt man \( n \ge 121 \).