Aufgabe:
Zeigen Sie mit einer Wahrheitstafel, dass die folgende Aussage allgemein giltig ist:
\( (\mathcal{A} \Rightarrow \mathcal{B}) \Leftrightarrow(\neg \mathcal{A} \vee \mathcal{B}) \)
Problem/Ansatz:
Text erkannt:
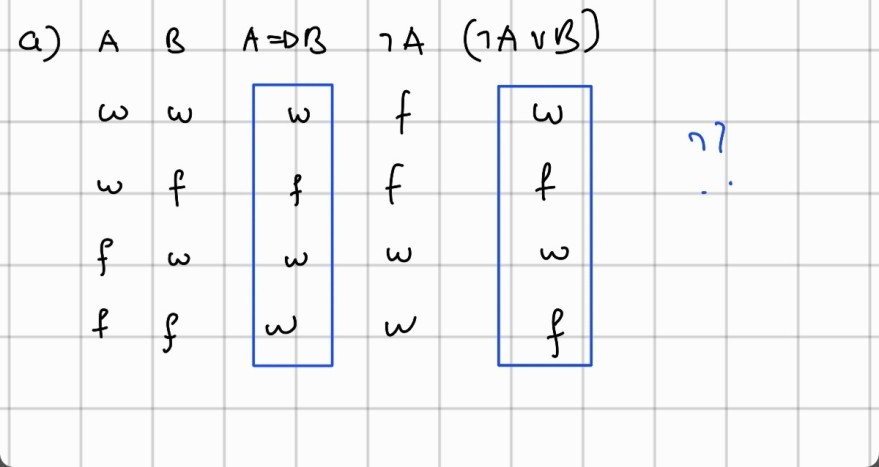
a) \( A B A \Rightarrow B \rightarrow A(\neg A \cup B) \)
\begin{tabular}{ll|l|l|l|}
\( \omega \) & \( w \) & \( \omega \) & \( f \) & \( \omega \) \\
\( w \) & \( f \) & \( f \) & \( f \) & \( f \) \\
\( f \) & \( \omega \) & \( w \) & \( \omega \) & \( w \) \\
\( f \) & \( f \) & \( w \) & \( w \) & \( f \) \\
\hline
\end{tabular}
Was genau hab ich falsch gemacht? Die Werte in den blauen Kästen sollten doch identisch sein..