Aufgabe:
Der Punk C(r/s) mit 0< r < 3 liegt auf dem Graphen einer Funktion f, der Punkt N(3/0) ist fest gewählt. C und N sind Eckpunkte eines Rechtecks. Die Funktion f ist gegeben durch f(x)= 1+ 1/5x^3
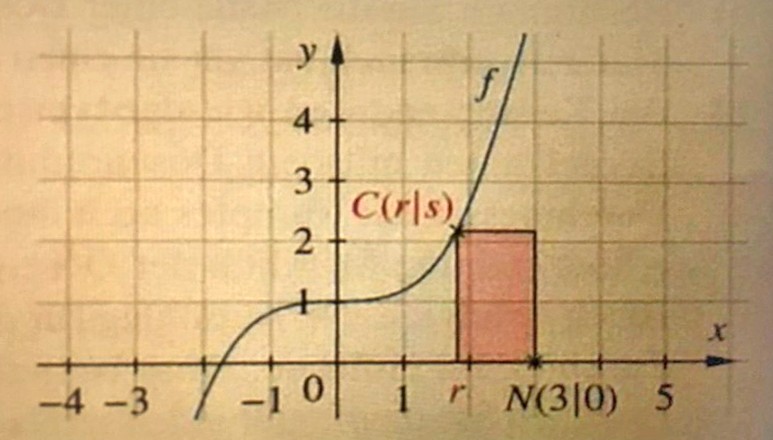
Zeigen Sie, dass für den Flächeninhalt A des Rechtecks gilt: A(r)=-1/5r^4 + 3/5r^3 - r + 3
Ermitteln Sie den maximalen Flächeninhalt des Rechtecks für 0 < r < 3
Problem/Ansatz:
< fehlt >