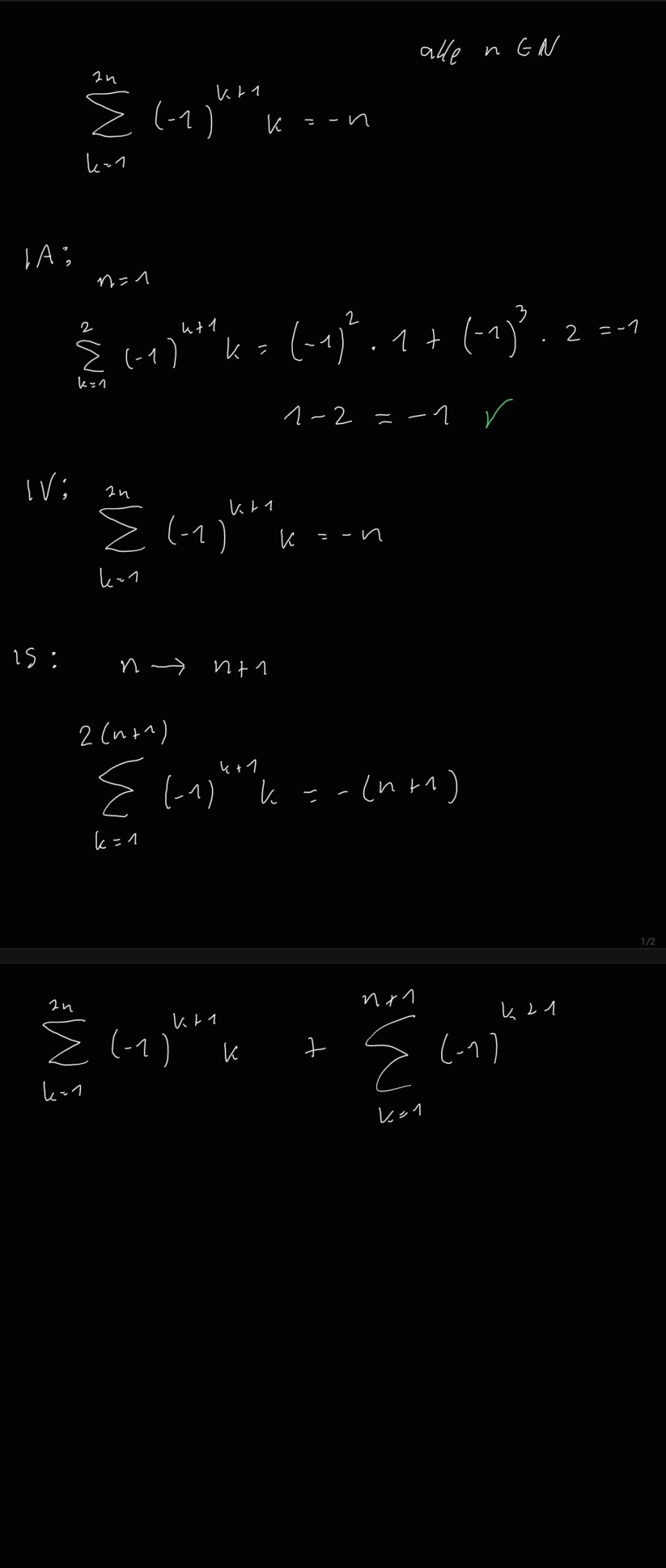
Text erkannt:
alle \( n \in N \)
\( \sum \limits_{k=1}^{2 n}(-1)^{k \cdot 1} k=-n \)
1A: \( n=1 \)
\( \sum \limits_{k=1}^{2}(-1)^{n+1} k=(-1)^{2} \cdot 1+(-1)^{3} \cdot 2=-1 \)
\( 1-2=-1 \quad r \)
IV; \( \sum \limits_{k=1}^{2 n}(-1)^{k \cdot+1} k=-n \)
is: \( \quad n \rightarrow n+1 \)
\( 2(n+1) \)
\( \sum \limits_{k=1}(-1)^{k+1} k=-(n+1) \)
\( \sum \limits_{k=1}^{2 n}(-1)^{k+1} k+\sum \limits_{k=1}^{n+1}(-1)^{k-2 \cdot 1} \)
Schrittmässig bin ich bis hier gekommen. Ich hätte noch erwähnen sollen, dass ich nebenei aus richtigen und falschen antworten eine Art "Induktionsschritt liste" erstellen soll. Ich orientiere mich daran zum Lernen:
Text erkannt:
Wählen Sie von diesen Sätzen:
Ihr Beweis:
\( \stackrel{I V}{=}-n+2 n+1-(2 n+2) \)
Wir beginnen mit dem Induktionsanfang: es gilt
\( \sum \limits_{k=1}^{1}(-1)^{k+1} k=(-1)^{2} \cdot 1=-1 \)
\( \begin{array}{c} \sum \limits_{k=1}^{2}(-1)^{k+1} k=(-1)^{2} \cdot 1+(-1)^{3} \cdot 2 \\ =1-2=-1 . \end{array} \)
\( =-n+2 n+1-2 n-2 \)
Also stimmt die Gleichung für \( n=1 \).
\( =-n+2 n+1-2 n+2 \)
Als nächstes führen wir den Induktionsschritt
\( =\sum \limits_{k=1}^{2 n}(-1)^{k+1} k+(-1)^{2 n+1}(2 n+1) \)
\( (n \rightarrow n+1) \) durch: aus der duktionsvoraussetzung \( (I V) \), d.h.
Dazu betrachten wir die folgende Rechnung:
\( \sum \limits_{k=1}^{2 n}(-1)^{k+1} k=-n \)
\( \sum \limits_{k=1}^{2(n+1)}(-1)^{k+1} k \)
folgern wir die Induktionsbehauptung, d.h. \( \sum \limits_{k=1}^{2(n+1)}(-1)^{k+1} k=-(n+1) \)
\( =-n-1=-(n+1) \)
\( =\sum \limits_{k=1}^{2 n}(-1)^{k+1} k \)
\( +(-1)^{2 n+2}(2 n+1)+(-1)^{2 n+3}(2 n+2) \)
Ich vermute was ich rechts eingetragen habe ist richtig aber weiterhin kann ich jetzt alles nicht eindeutig zuordnen
Mfg ✌️