Aufgabe
Ich habe als Aufgabe die Nummer 2 und 4 bloß habe ich das ganze nicht so richtig verstanden und würde mich über eine hilfe sehr freuen
Problem/Ansatz:
…
Ich weiß nicht wie ich genau vorangehen soll
Text erkannt:
Aufgabe 2
Aus einer Urne, die 3 schwarze und 5 weiße Kugeln enthält, wird dreimal hintereinander eine Kugel gezogen und wieder zurückgelegt.
a) Stellen Sie den Zufallsversuch in einem Baumdiagramm dar.
b) Ermitteln Sie die Wahrscheinlichkeit, mit der
ba) zwei schwarze und eine weiße Kugel
bb) mindestens eine weiße Kugel
bc) mindestens zwei weiße Kugeln gezogen werden
d)
Aufgabe 4
Aus einer Urne, die 2 blaue, 2 rote und 3 gelbe Kugeln enthält, wird dreimal nacheinander eine Kugel gezogen. Fertigen Sie ein Baumdiagramm an für den Fall, dass die Kugeln
a) immer wieder zurückgelegt werden (vgl. Vorlage zum Baumdiagramm auf S. 4)
b) nicht zurückgelegt werden (vgl. Vorlage zum Baumdiagramm auf S. 5)
Berechnen Sie die Wahrscheinlichkeit, dass
c) zwei blaue und eine rote Kugel gezogen werden
d) jeweils eine Kugel von jeder Farbe gezogen wird
Text erkannt:
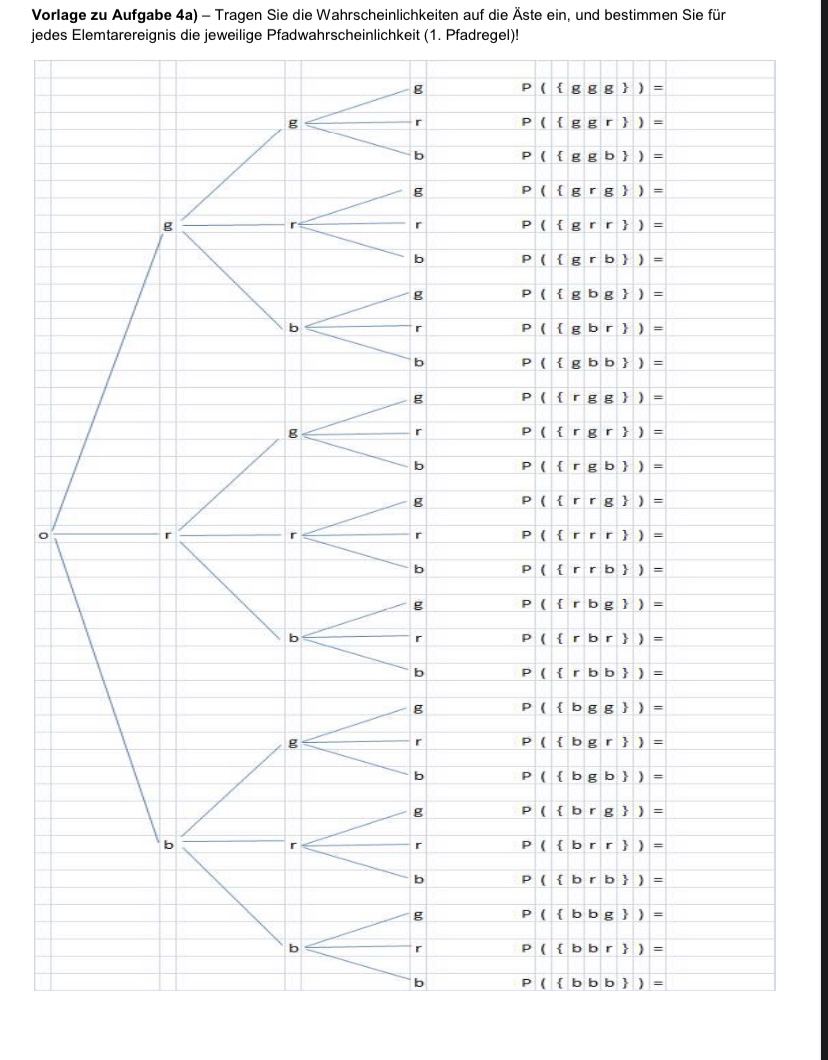
Vorlage zu Aufgabe 4a) - Tragen Sie die Wahrscheinlichkeiten auf die Äste ein, und bestimmen Sie für jedes Elemtarereignis die jeweilige Pfadwahrscheinlichkeit (1. Pfadregel)!

Text erkannt:
Vorlage zu Aufgabe 4b) - Tragen Sie die Wahrscheinlichkeiten auf die Äste ein, und bestimmen Sie für jedes Elemtarereignis die jeweilige Pfadwahrscheinlichkeit (1. Pfadregel)!