Abstand zweier Punkte im Raum - Bestimmung der Koordinaten der Eckpunkte → quadratische Pyramide

Question

Hallo ihr Lieben,

ich habe ein kleines Problem in Mathe bzgl. Abstand zweier Punkte im Raum:

Die Aufgabe:

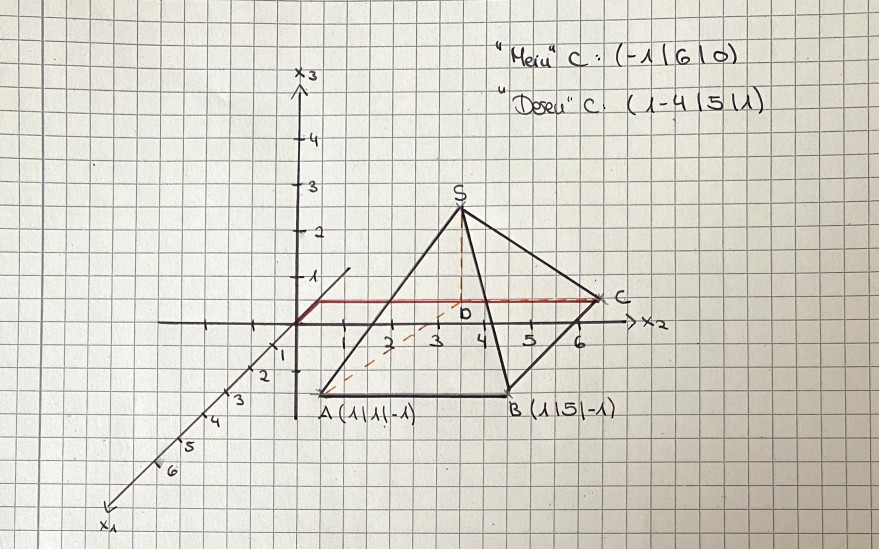
Gegeben ist eine senkrechte quadratische Pyramide mit den Eckpunkten A, B, C, D. Die Höhe der Pyramide ist h = 3

a) Bestimmen Sie die Koordinaten der Eckpunkte C und D und der Spitze S.

Ich habe euch die Aufgabe beigefügt. Bei mir kam bei C raus: C (-1 | 6 | 0). Die Lösungen sagen allerdings: C (1-4 | 5 | 1).

Jetzt bin ich irritiert, warum man die x1-Achse nicht in den Minusbereich abzählen kann und dann auf der x2-Achse direkt nach rechts zählen kann, sondern erst die x1-Achse in den positiven Bereich zählen muss und dann wieder -4 rechnet.

Ist das immer so oder nur bei dieser Pyramide? Ist das ein Fehler vom Buch?

LG, Lucy

Comments

Da fehlt noch ein Teil der Aufgabenstellung! Ich nehme an, dass die Punkte \(A\) und \(B\) gegeben sind - oder?

Liegt die Grundfläche der Pyramide parallel zur xy-Ebene ? Oder ist der Punkt \(S\) gegeben?

Kann es sein, dass \(C\) bei \(C=(-3|5|{\color{red}-1})\) liegt?

Answer 1

Deine Pyramide ist aus dem Winkel, Seitenlänge Δy B-A = 4

C:=B +(-4,0,0)

D:=A+(-4,0,0)