Was bedeuten die senkrechten Striche also die Pipes?

Question

Ich arbeite grad ein Beispiel für einen Beweis durch.

Hierbei sind bspw. die Diagonalen von senkrechten Strichen - Pipes - umschlossen.

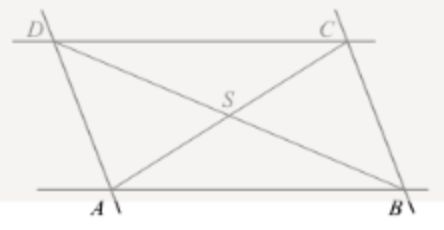
Wir betrachten die Diagonalen (Geraden \( A C \) und \( B D \) ) und ihren Schnittpunkt \( S . \)

- Nach dem Wechselwinkelsatz gilt $$ \angle(A B D) \equiv \angle(C D B) $$

- Nach dem Wechselwinkelsatz gilt $$ \angle(A D B)=\angle(C B D) $$

- Trivialerweise ist \( |B D|=|B D| \)

- Daher sind nach dem Kongruenzsatz WSW" \( \Delta A B D \) und \( \Delta C D B \) kongruent.

- Somit gilt \( |A B|=|C D| \) sowie \( |A D|=\mid B C \).

Wofür stehen die Pipes?

Answer 1

| | sind Betragsstriche, die stehen für die Länge der Strecke / oder des Vektors.

In der Grundschule wird dafür eher ein Querstrich über BD benutzt. Das geht auf der Tastatur schlecht.