Berechnen Sie die fehlenden Koordinaten (Lineare Funktion)

Question

Aufgabe:

Die Punkte P(6/5 | a) und Q(b|-2) liegen auf dem Grafen der Funktion F mit der Gleichung

f(x)= -1/3x+2

Berechnen Sie die fehlenden Koordinaten

Problem/Ansatz:

Ich weiß nicht was mit fehlenden Koordinaten gemeint ist und wie genau ich das berechnen soll

Answer 1

"Die Punkte P(6/5 | a) und Q(b|-2) liegen auf dem Grafen der Funktion F mit der Gleichung  f(x)= -1/3x+2"

f(x)= -1/3x+2

f(6/5)= -1/3*6/5+2=8/5=1,6  →  P(6/5 | 1,6)

f(x)= -1/3x+2

f(b)= -1/3*b+2=-2  →   -1/3*b=-4        1/3*b=4     b=12   →Q(12|-2)

Comments

Vielen lieben Dank. Jetzt habe ich das verstanden!

Answer 2

Hallo,

ein Punkt hat zwei Koordinaten, x und y.

\(f(x)=\frac{1}{3}x+2\)

Der Punkt P liegt beispielsweise auf dieser Geraden. 3 ist die x-Koordinate, 1 die y-Koordinate

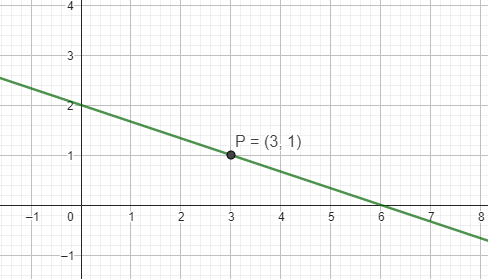
Wenn du die y-Koordinate eines Punktes bestimmen willst, setzt du für x die x-Koordinate ein und rechnest aus.

Wenn du die x-Koordinate eines Punktes bestimmen willst, setzt du für f(x) die y-Koordinate ein und löst nach x (hier b) auf.

Gruß, Silvia

Comments

Danke für die Antwort, aber wie haben sie den Koordinaten P= (3/1) herausgefunden?

---

Ich wollte dir damit nur ein Beispiel geben, damit klar ist, was die Koordinaten eines Punktes sind. Also habe ich 3 für x in die Gleichung eingesetzt. Das Ergebnis = f(3) ist 1. So geht man z.B. vor, wenn man eine Wertetabelle erstellen will.

Für x hätte ich natürlich auch eine andere Zahl einsetzen können.

---

Danke für die Antwort aber ich verstehe es leider immer noch nicht und wie sie auch auf die 3 gekommen sind

---

Statt f(x) kannst du auch y schreiben. Dann sieht deine Gleichung so aus:

\(\blue y=-\frac{1}{3}\red x+2\)

Ich hatte mir 3 für x ausgedacht. Hier in deiner Aufgabe ist x = \( \red{\frac{6}{5}} \)

Eingesetzt in die Gleichung ergab bei mir

\(\blue y=-\frac{1}{3}\cdot \red 3+2=-1+2=\blue 1\)

Damit kam ich auf \(P(\red3|\blue1)\)

Was musst du also tun?