Bestimmen Sie die globale Lösung von (P) .

Question

Aufgabe:

Gegeben Sei das nichtlineare Optimierungsproblem \( (P) \) :
\( \begin{aligned} \min & x+y \\ \text { s.t. } & x^{2}-2 x+1+y^{2} \leq 1 \\ &(x+1)^{2}-1 \leq-y^{2} \end{aligned} \)
(a) Bestimmen Sie die globale Lösung von \( (P) \).

Problem/Ansatz:

habe raus das es keine KKT Punkte hat aber wie komme ich jetzt auf die globale Lösung?

Answer 1

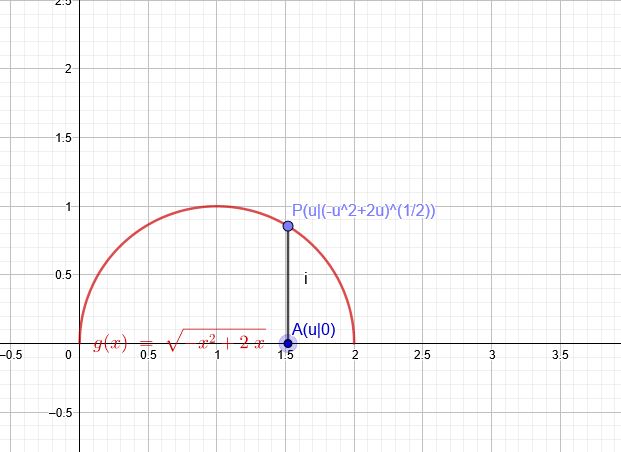
\(f(x,y)=x+y\) soll minimal werden.

\(x^2-2x+1+y^2≤1\)

\(P(u)\) liegt auf \(y= \sqrt{-x^2+2x} \)   →\(v= \sqrt{-u^2+2u} \)

\(f(u)=u+ \sqrt{-u^2+2u}\)

\(f´(u)=1- \frac{2-2u}{2*\sqrt{-u^2+2u}}\\ =1- \frac{1-u}{\sqrt{2u-u^2}}    \)

\(1- \frac{1-u}{\sqrt{2u-u^2}} =0   \)

\(\sqrt{2u-u^2} =1-u   |^{2} \)

\(2u-u^2 =1-2u+u^2   \)

\(4u-2u^2 =1  \)

\(u^2-2u =-\frac{1}{2}  \)

\((u-1)^2 =-\frac{1}{2}+1 =\frac{1}{2}  |\sqrt{~~}  \)

1.)

\(u-1 =\frac{1}{2} *\sqrt{2}  \)

\(u_1 =1+\frac{1}{2} *\sqrt{2}  \) →\(v_1= \sqrt{-(1+\frac{1}{2} *\sqrt{2})^2+2*(1+\frac{1}{2} *\sqrt{2}})=\frac{1}{2}*\sqrt{2} \)→maximaler Wert

2.)

\(u-1 =-\frac{1}{2} *\sqrt{2}  \)

\(u_2 =1-\frac{1}{2} *\sqrt{2}  \)  →\(v_2= \sqrt{-(1-\frac{1}{2} *\sqrt{2})^2+2*(1-\frac{1}{2} *\sqrt{2}}) =\frac{1}{2}*\sqrt{2}\) minimaler Wert