Aufgabe:
\(\begin{array}{l} \max _{S C}=m(a-b(c+m)+\alpha \theta)-I \theta^{2} \Phi \\ \frac{\Delta}{\Delta m} \pi_{S C}=a-2 b m-b c+\alpha \theta \Phi \\ \text { Undף } \\ \frac{\Delta}{\Delta \theta} \pi_{S C}=m \alpha-2 I \theta \uparrow \end{array} \)
Entscheidungsvariablen \( \cdot \) kann \( \cdot \) festgestellt'werden, 'wie \( \cdot \) wir \( \cdot \) in \( \cdot \) den \( \cdot \) folgenden \( \cdot \) Ergebnissen \( \cdot \) Lösen ·der'Gleichungen, bei \( \cdot \) gleichzeitigem Lösen, 'erhalten 'wirๆ
\( m^{*}=\frac{2 I(a-b c)}{4 I b-\alpha^{2}} \Phi \)
Und
\( \theta^{*}=\frac{\alpha(a-b c)}{4 I b-\alpha^{2}} \uparrow \)
Problem/Ansatz:
Guten Abend an alle,
ich habe die oben abgebildete Aufgabe händisch abgetippt aus einem Paper, ich hoffe das ich hier nicht gegen irgendwelche Regeln verstoße. Wir sehen eine Gewinnfunktion einer Supply Chain in einem zentralen Setting, sprich es gibt nur einen Entscheidungstreffer. Nun wird die Gewinnfunktion einmal nach m & einmal nach Theta abgeleitet, soweit keine Probleme. Wenn ich mir jedoch m* und Theta* anschaue, dann versteh ich nicht, wie diese entstehen. Unten mein Ansatz, ich erhalte gänzlich andere Gleichungen. Mein Verdacht liegt darin, dass m* & Theta* dadurch zustande kommen, dass ich die beiden ersten Ableitungen erst gleich 0 und dann gleichsetze. Die Gleichung einmal nach m & einmal nach Theta umstelle & die umgestellte m Gleichung in die umgestellte Theta Gleichung einsetze. Das würde erklären warum bei m* Theta wegfällt & umgekehrt. Wenn ich das jedoch versuche, scheitere ich kläglich....
Unten stehend mein Ansatz:
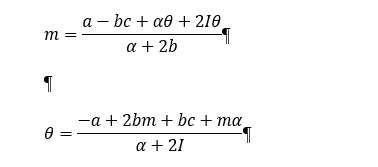
Text erkannt:
\( m=\frac{a-b c+\alpha \theta+2 I \theta}{\alpha+2 b} \)
๔
\( \theta=\frac{-a+2 b m+b c+m \alpha}{\alpha+2 I} \)
Wenn ich m jetzt in Theta einsetzen würde, dann würde die Gleichung wie folgt aussehen:
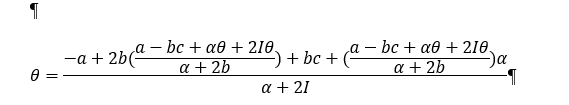
Text erkannt:
\( \theta=\frac{-a+2 b\left(\frac{a-b c+\alpha \theta+2 I \theta}{\alpha+2 b}\right)+b c+\left(\frac{a-b c+\alpha \theta+2 I \theta}{\alpha+2 b}\right) \alpha}{\alpha+2 I} \)
Wer soll das denn lösen können?