Integral Funktionen und Rechnungen

Question

H

Hallo, ich wollte fragen, ob jemand mir helfen kann.

Answer 1

b)Gerade durch \(P(5|1,5) \)  mit    \(m=0,5\)

\( \frac{y-1,5}{x-5}=0,5 \)

\(y-1,5=0,5*(x-5)=0,5x-2,5 \)

\(y=0,5x-1\)

Parabelgleichung:

\(y=a*(x-3)^2+1\)    \(P(5|1,5)\)

\(1,5=a*(5-3)^2+1=4a+1\)      \(4a=0,5\)     \(a=\frac{0,5}{4}=\frac{1}{8}\)

\(y=\frac{1}{8}*(x-3)^2+1\)

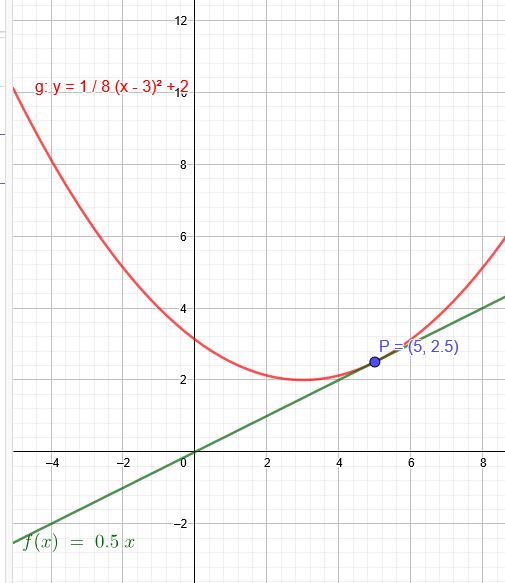
Ich verschiebe beide Funktionen um 1 Einheit nach oben:

\(y=0,5x\)  und \(p(x)=\frac{1}{8}*(x-3)^2+2=\frac{1}{8}(x^2-6x+9)+2)\)

\( \int\limits_{0}^{5}[\frac{1}{8}*(x^2-6x+9)+2]*dx\)=

=\(\frac{1}{8}*\frac{x^3}{3}-\frac{1}{8}*\frac{6x^2}{2}+\frac{1}{8}*9x +2x\)=

=\(\frac{x^3}{24}-\frac{3*x^2}{8}+\frac{9x}{8}+2x=\frac{x^3}{24}-\frac{3*x^2}{8}+\frac{25x}{8}\)

In den Grenzen 5 und 0:

\(\frac{5^3}{24}-\frac{3*5^2}{8}+\frac{25*5}{8}=\frac{5^3}{24}-\frac{3*3*5^2}{24}+\frac{3*25*5}{24}=\frac{5^3}{24}-\frac{3*3*5^2}{24}+\frac{3*5^3}{24}=\frac{4*5^3}{24}-\frac{9*5^2}{24}\)

Grenze 0 ergibt 0

Fläche unter der Geraden:

\( \int\limits_{0}^{5}0,5x*dx=0,5*\frac{x^2}{2}=\frac{x^2}{4}\)

In den Grenzen 5 und 0:

\( \frac{5^2}{4}=\frac{6*5^2}{24}\)

Diese Fläche muss nun von der Fläche unter der Parabel abgezogen werden:

Gesuchte Fläche :

\(A=\frac{4*5^3}{24}-\frac{9*5^2}{24}-\frac{6*5^2}{24}=\frac{4*5^3}{24}-\frac{15*5^2}{24}=\frac{125}{24}FE\)

Comments

9a)

Geradengleichung durch A und B mit der Achsenabschnittsform einer Geraden:

\( \frac{x}{a}+\frac{y}{b}=1 \)

\(a=1\)   und   \(b=\frac{1}{2}\)

\( \frac{x}{1}+\frac{y}{\frac{1}{2}}=1 \)      \( \frac{y}{\frac{1}{2}}=1-x|*\frac{1}{2} \)

\(y=-\frac{1}{2}* x+\frac{1}{2}\)

Die 2.Gerade:  \(y=x-4\)

Ich verschiebe die 3 Graphen um 1 Einheit nach oben:

1.)  \(y=-\frac{1}{2}* x+\frac{3}{2}\)

2.) \(y=x-3\)

3.) \( \sqrt{x+2}+1 \)

\(A₁= \int\limits_{-1}^{3}f(x)*dx \)

\(A₂= \int\limits_{3}^{7}g(x)*dx \)

\(A₃= \int\limits_{-1}^{7}h(x)*dx \)

\(A₃= \int\limits_{-1}^{7}(\sqrt{x+2}+1)*dx \)

Substituiere \(x+2=u\) →  \(\sqrt{u}=u^{\frac{1}{2}}\)

..........................

Gesuchte Fläche:\(A₃-A₂- A₁\)

Answer 2

Gegenfrage: Kannst du die Gleichungen der beteiligten Geraden in Aufgabe a) selbst aufstellen?

Wenn du mal in Klasse 8 (weiß ich nicht) warst, sollte das möglich sein.

Weiter: Kannst du bei Kenntnis der Steigung einer Geraden und eines Punktes, der auf dieser Geraden liegt, die Geradengleichung bestimmen?

Vorher brauchen wir an Flächenberechnungen überhaupt keinen Gedanken zu verschwenden.