Verlauf der Hyperbel mit steigendem Exponenten

Question

Aufgabe:

Verlauf der Hyperbel mit steigendem Exponenten

Problem/Ansatz:

f(x)= 1/x^n mit n ungerade

f(x)= 1/x^n mit n gerade

Answer 1

mit n ungerade   ich wähle n ∈ ℕ₀

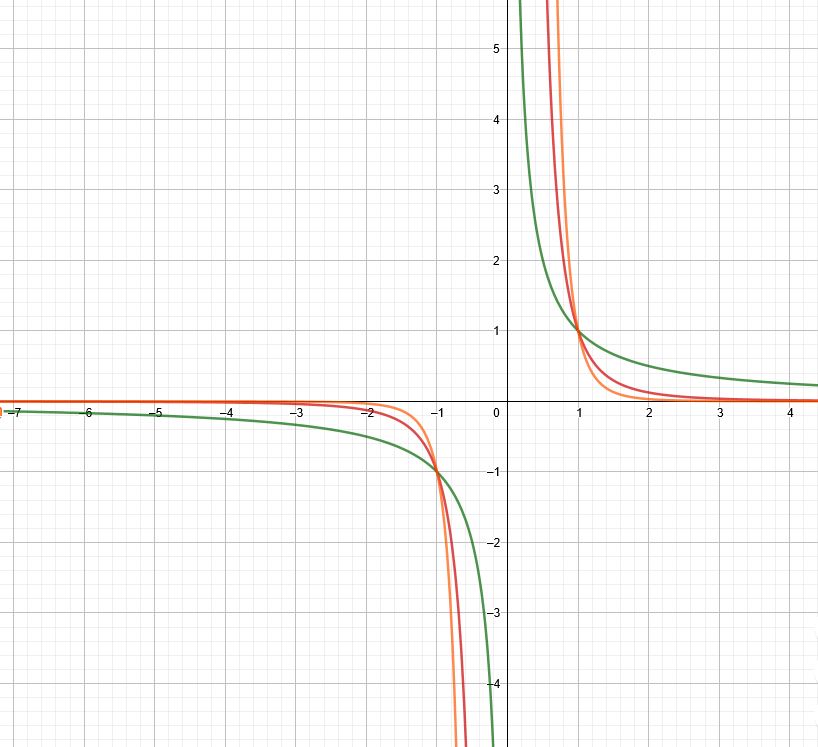
\(f(x)=  \frac{1}{x^{1}} \)  mit grün dargestellt

_{\(f(x)=  \frac{1}{x^{3}} \) mit rot dargestellt}

_{\(f(x)=  \frac{1}{x^{5}} \) mit orange}  dargestellt

mit n gerade   ich wähle n ∈ ℕ0

\(f(x)=  \frac{1}{x^{0}}=1 \)  mit grün dargestellt

\(f(x)=  \frac{1}{x^{2}} \) mit rot dargestellt

\(f(x)=  \frac{1}{x^{4}} \) mit orange dargestellt

Comments

Und was kann man anhand den Verläufen feststellen wenn der Exponent steigt ?

---

Kann man schreiben das die Hyperbel mit steigenden ungeraden Exponent gestreckter verläuft?