Guten Tag, ich stecke leider bei folgender Aufgabe fest und weiß nicht wie ich hier richtig verfahren soll, wäre sehr hilfreich wenn jemand hierfür passende Lösungsansätze mitteilen könnte.
Aus drei Brettern der Breite g soll ein Kanal mit maximalem Fassungsvermögen gebaut werden. Hierfür muss der Flächeninhalt Q des trapezförmigen Querschnittes des Kanals maximiert werden (vgl. Skizze). Wie muss der Winkel α (in der Skizze) gewählt werden, damit der Flächeninhalt Q maximal wird? Gehen Sie zur Lösung des Problems wie folgt vor:
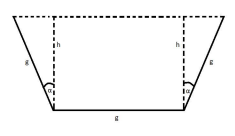
(i) Begründen Sie, dass der Flächeninhalt Q (mit den Bezeichnungen aus der Skizze) gegeben ist durch Q = gh(1 + sin(α)).
(ii) Beschreiben Sie Q als Funktion einer Variablen, indem Sie die Höhe h in Abhängigkeit des Winkels α ausdrücken und überlegen Sie sich einen geeigneten Parameterbereich für α.
iii) Führen Sie die notwendige Bedingung für ein Maximum (im Inneren des Parameterbereiches) auf die Gleichung
2x2 + x - 1 mit x = sin(α) zurück und lösen Sie diese unter den gegebenen Nebenbedingungen.
iv) Aus Teil (iii) erhalten Sie als einzigen Kandidaten den Winkel α = π/6. Überprüfen Sie, ob es sich hierbei tatsächlich um die Lösung des gegebenen Maximierungsproblems handelt und bestimmen Sie den maximalen Flächeninhalt für Q.