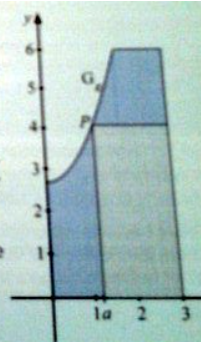
Die schraffierte Fläche in dem abgebildeten Diagramm stellt den Rest einer längs eines Parabelstücks zersprungenen Glasplatte dar. Der zu diesem Parabelstück gehörende Funktionsterm lautet:
\( S(x)=x^{2}+\frac{1}{3}, \quad D_{g}=\left[0 ; \sqrt{\frac{10}{3}}\right) \)
Aus dem Rest der Platte soll eine rechteckige Schebe wie abgebildet so geschnitten werden, dass der Punkt \( P(a ; g(a)) \) auf \( G_{x} \) liegt. (nach Abschlussprufung 2003 Al)
a) Stellen Sie die Maßzahl \( A(a) \) der Rechtecksfläche in Abhängigkeit von \( a \) dar. Geben Sie \( D_{A} \) an.
b) Zeichnen Sie den Graphen \( \mathrm{G}_{A} \).