matrix Gleichung lösen, ? wäre sehr dankbar

Question

Aufgabe:

Text erkannt:

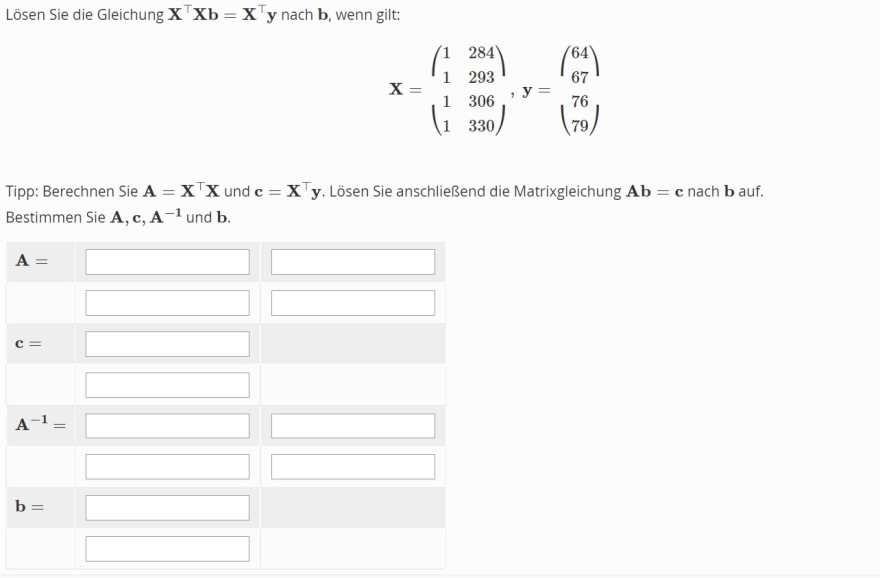
Lösen Sie die Gleichung \( \mathbf{X}^{\top} \mathbf{X} \mathbf{b}=\mathbf{X}^{\top} \mathbf{y} \) nach \( \mathbf{b} \), wenn gilt:
\( \left.\mathbf{X}=\left(\begin{array}{ll} 1 & 284 \\ 1 & 293 \end{array}\right),\left(\begin{array}{ll} 1 & 306 \\ 1 & 330 \end{array}\right), \mathbf{y}=\begin{array}{l} 64 \\ 67 \end{array}\right) \)
Tipp: Berechnen Sie \( \mathbf{A}=\mathbf{X}^{\top} \mathbf{X} \) und \( \mathbf{c}=\mathbf{X}^{\top} \mathbf{y} \). Lösen Sie anschließend die Matrixgleichung \( \mathbf{A} \mathbf{b}=\mathbf{c} \) nach \( \mathbf{b} \) auf. Bestimmen Sie \( \mathbf{A}, \mathbf{c}, \mathbf{A}^{-1} \) und \( \mathbf{b} \).
\( \mathbf{A}= \)
\( \mathbf{c}= \)
\( \mathbf{A}^{-1}= \)
\( \mathbf{b}= \)

Problem/Ansatz:

hallo, 3 aufgaben habe ich schon gelöst, da komme ich aber nicht weiter. Könnte mir jemand helfen?

Answer 1

Hallo Jenny,

es ist:$$A= X^T\cdot X = \begin{pmatrix}4& 1213\\ 1213& 369041\end{pmatrix}\\ c = X^T \cdot y = \begin{pmatrix}286\\ 87133\end{pmatrix} \\ A^{-1} = \frac{1}{4795}\begin{pmatrix}369041& -1213\\ -1213& 4\end{pmatrix} \\ b = \frac{1}{4795}\begin{pmatrix}-146603\\ 1614\end{pmatrix}$$Gruß Werner

Comments

Danke sehr :)

---

das stimmt leider nicht :( ist nicht korrekt

---

das stimmt leider nicht :( ist nicht korrekt

woraus schließt Du das?

das sieht aber ziemlich richtig aus. Ich habe das ganze nochmal mit Excel überprüft. Die Ergebnisse stimmen mit meinen exakt überein.

Wenn man den Achsenabschnitt \(b\) (alias \(b_1\) und die Steigung \(m\) (alias \(b_2\)) der Geraden näherungsweise angibt, kommt man zu$$b=−30,5741397289\\m=0,336600625652$$Vielleicht liegt's am Dezimaltrenner (Komma oder Punkt) oder geforderten Anzahl der Nachkommastellen?

---

da ich Vorbereitung für Klausur gemacht habe, Selbsttest gelöst und da ich genauso die Ergebnisse eingegeben und leider keine Punkte erhalten. es kann auch Systemfehler sein. :(

werde nächste Woche Prof. fragen

danke sehr