Zeifen dass ein Körper und ob echte teilmenge

Question

Aufgabe:

Siehe Foto:

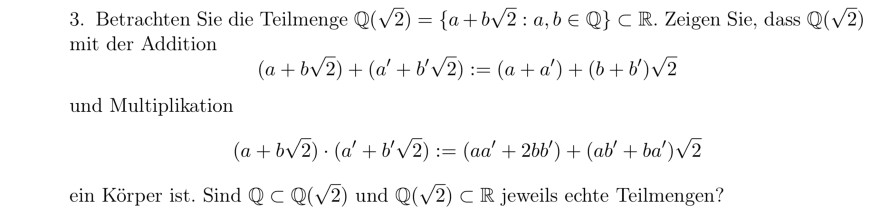
Text erkannt:

3. Betrachten Sie die Teilmenge \( \mathbb{Q}(\sqrt{2})=\{a+b \sqrt{2}: a, b \in \mathbb{Q}\} \subset \mathbb{R} \). Zeigen Sie, dass \( \mathbb{Q}(\sqrt{2}) \) mit der Addition
\( (a+b \sqrt{2})+\left(a^{\prime}+b^{\prime} \sqrt{2}\right):=\left(a+a^{\prime}\right)+\left(b+b^{\prime}\right) \sqrt{2} \)
und Multiplikation
\( (a+b \sqrt{2}) \cdot\left(a^{\prime}+b^{\prime} \sqrt{2}\right):=\left(a a^{\prime}+2 b b^{\prime}\right)+\left(a b^{\prime}+b a^{\prime}\right) \sqrt{2} \)
ein Körper ist. Sind \( \mathbb{Q} \subset \mathbb{Q}(\sqrt{2}) \) und \( \mathbb{Q}(\sqrt{2}) \subset \mathbb{R} \) jeweils echte Teilmengen?

Answer 1

Hallo

nacheinander die Körperaxiome zeigen, dabei kannst du die für reelle Zahlen voraussetzen musst also  im Wesentlichen nur zeigen dass Produkt und Summe wieder in diesem K liegen, ebenso wie das Inverse.

Gruß lul