Hallo, ich bin grad in der Vorbereitung auf meine LK Q3 Klausur.
Bei einer Aufgabe komme ich nicht so ganz weiter.
Sie lautet: Die Ebene E ist orthogonal zur Ebene F: 2x-4z=6 Die Gleichung g: x=(1, 2, -1) + r (-2, -2, 1) stellt die Schnittgerade von E und F dar. Stellen Sie die Normalengleichung von E auf.
Ich hatte eine Ebene E berechnet, wenn ich die Ebene F und die Gerade g in GeoGebra eintippe, stellt die Gerade aber gar keine Schnittgerade mit Ebene F dar.
Die rote Ebene stellt die gegebene Ebene F dar: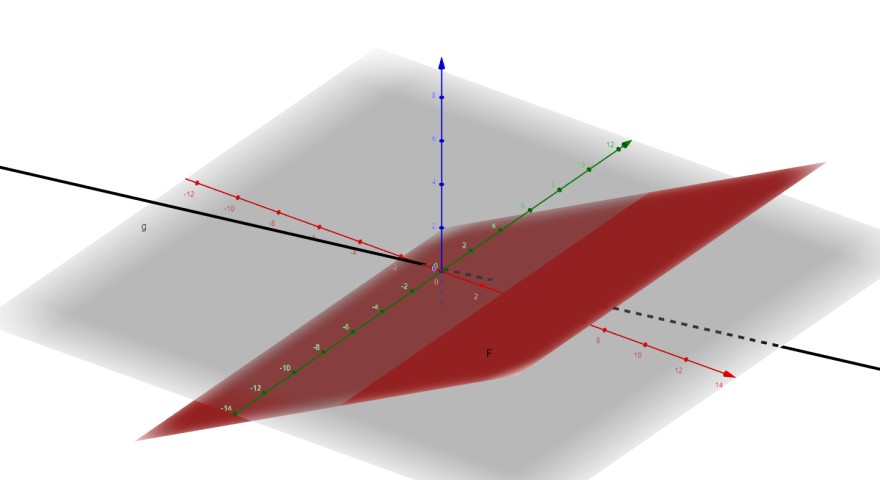
Die Gerade g schneidet die Ebene F ja nur.
Auf dieser Grafik ist die von mir errechnete Ebene E noch zu sehen:
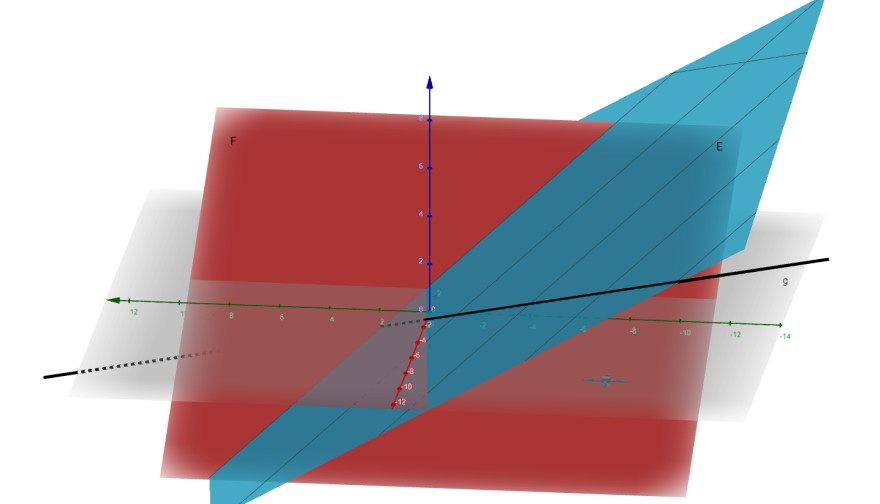Die Gerade liegt auf der von mir errechneten Ebene.
(Die von mir errechnete Ebene hat Gleichung:
E: x= (1, 2, -1) + r * (-2, -2, 1) + s * (-9, 4, -3)
Die Gerade verläuft auf dieser Ebene, ich kann mir aber nicht erklären warum die Gerade nicht auf der gegebenen Ebene liegt.
Kann mir da jemand weiterhelfen?
