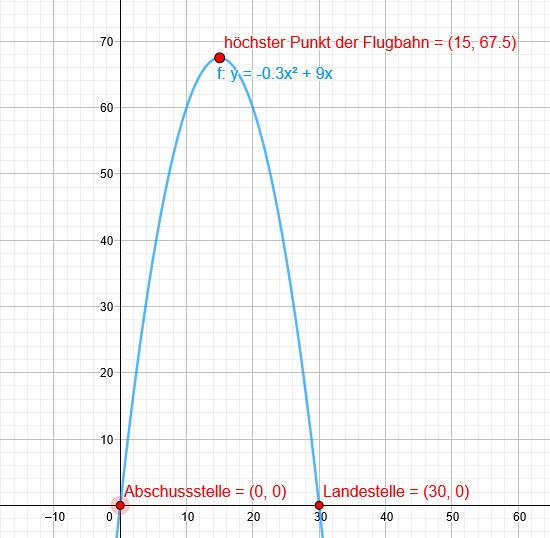
Der Graph, der quadratischen Funktion mit der Funktionsgleichung \(y=-0,3x^2+9x\)
a) notiere zunächst die zugehörige quadratische Gleichung. Berechne anschließend, in welcher Entfernung von der Abschussstelle die Rakete wieder auf dem Erdboden auftritt.
b) Bestimme den höchsten Punkt der Flugbahn
\(y=-0,3x^2+9x\)
zugehörige quadratische Gleichung:
\(-0,3x^2+9x=0\)
Entfernung zur Abschussstelle:
\(-0,3x^2+9x=0|:(-0,3)\)
\(x^2-30x=0\)
\(x*(x-30)=0\)
\(x₁=0\) Abschussstelle
\(x₂=30\)Landestelle
b)höchster Punkt der Flugbahn:
\(y=-0,3x^2+9x\)
\(y´=-2*0,3x+9\)
\(-2*0,3x+9=0\)
\(2*0,3x=9\) \(0,3x=4,5\) \(x=\frac{4,5}{0,3}=\frac{45}{3}=15\)
\(y(15)=-0,3*15^2+9*15=67,5\)