Bestimmen Sie a, b, c . Polynomdivision komplexer Zahlen

Question

Aufgabe:

Hey Leute,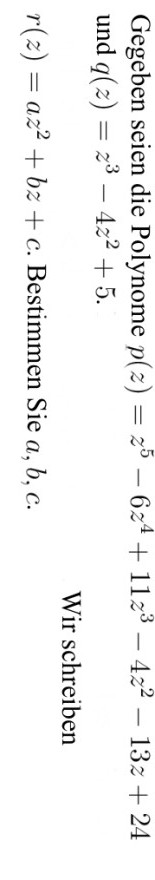

Text erkannt:

Gegeben seien die Polynome \( p(z)=z^{5}-6 z^{4}+11 z^{3}-4 z^{2}-13 z+24 \) und \( q(z)=z^{3}-4 z^{2}+5 \).
Wir schreiben
\( r(z)=a z^{2}+b z+c \). Bestimmen Sie \( a, b, c \).

stimmt es wie ich es gelöst habe?

Problem/Ansatz:

Ich mache zunächst  die Polynomdivision. Danach bekomme ich dies heraus: z^2-2z+3(3z^2-3z+9)/(z^3-4z^2+5)

Wäre dann die Lösung: r(z)=z^2-2z-3 ? Wenn nein was lautet die Lösung und warum?

Answer 1

Bestimmen Sie \( a, b, c \).

Wäre dann die Lösung: r(z)=z²-2z-3

Nein. Die Lösung hat die Form "a hat den Wert ... und b hat den Wert ... und c hat den Wert ...".

Außerdem ist aus der Aufgabenstellung nicht ersichtlich, wie \(p\), \(q\) und \(r\) zusammenhängen sollen.

Ich vermute es soll \(p(x) = q(x)\cdot g(x) + r(x)\) für ein Polynom \(g(x)\) mit \(\operatorname{Grad}(q) > \operatorname{Grad}(r)\) sein. Dann wäre \(r(z)=z^2-2z-3\) falsch.